题目内容
(本小题满分12分)
已知等差数列{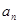 }的前项和为
}的前项和为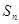 ,且
,且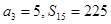 。数列
。数列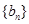 为等比数列,且首项
为等比数列,且首项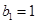 ,
,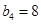 .
.
(1)求数列 ,
,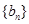 的通项公式;
的通项公式;
(2)若数列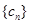 满足
满足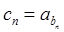 ,求数列
,求数列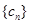 的前
的前 项和为
项和为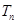 ;
;
(1)
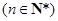 . (2)
. (2)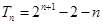 .
.
解析试题分析:(1)设首项为a1,公差为d,由题意,得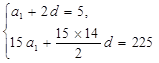 ,得到首项和公差,进而得到等比数列的通项公式。
,得到首项和公差,进而得到等比数列的通项公式。
(2)分析可知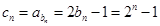 ,那么利用等比数列的求和得到结论。
,那么利用等比数列的求和得到结论。
解:(1)设首项为a1,公差为d,由题意,得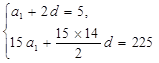
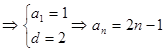 ……3分
……3分
又 数列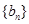 为等比数列,设公比为
为等比数列,设公比为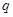 ,
,
∵ 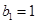 ,
,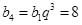 ,
,
∴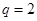 .∴
.∴ 
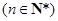 . …6分
. …6分
(2)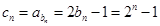 . 8分
. 8分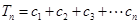

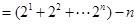
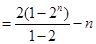
所以 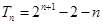 . …12分
. …12分
考点:本题主要考查等差数列和等比数列的通项公式的求解和求和公式的运用。
点评:解决该试题的关键是能熟练的运用等差数列和等比数列的通项公式来求解其基本量,进而得到数列的求和。

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
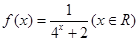 .
.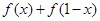 的值;
的值;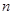 项和公式的推导方法,求:
项和公式的推导方法,求: 的值.
的值.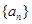 的前
的前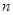 项和为
项和为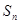 ,且
,且
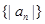 的前
的前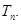
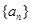 中,
中,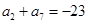 ,
,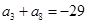 .
.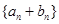 是首项为
是首项为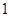 ,公比为
,公比为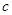 的等比数列,求
的等比数列,求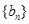 的前
的前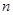 项和
项和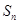 .
. 、
、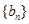 满足
满足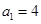 ,
,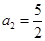 ,
,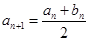 ,
,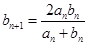 .
. 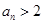 ,
,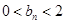 (
( );
);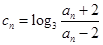 ,求数列
,求数列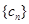 的通项公式;
的通项公式;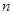 项和为
项和为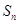 ,数列
,数列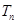 ,数列
,数列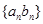 的前
的前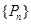 ,求证:
,求证: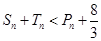 .
.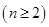
 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列 为等差数列,且
为等差数列,且 。
。 求证:数列
求证:数列 若
若 ,
, 为数列
为数列 的前
的前 的前四项和为10,且
的前四项和为10,且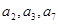 成等比数列
成等比数列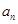
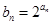 ,求数列
,求数列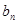 的前
的前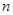 项和
项和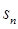 。
。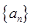 的前n项和
的前n项和 (n为正整数)。
(n为正整数)。 ,求证数列
,求证数列 是等差数列,并求数列
是等差数列,并求数列 ,
, ,求
,求 .
. 中,
中, ,
,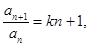

 ;(2)求数列
;(2)求数列 的前
的前 项和。
项和。