题目内容
定义在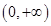 上的函数
上的函数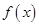 ,如果对任意
,如果对任意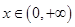 ,恒有
,恒有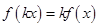 (
(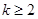 ,
,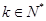 )成立,则称
)成立,则称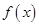 为
为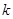 阶缩放函数.
阶缩放函数.
(1)已知函数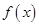 为二阶缩放函数,且当
为二阶缩放函数,且当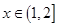 时,
时,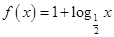 ,求
,求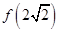 的值;
的值;
(2)已知函数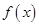 为二阶缩放函数,且当
为二阶缩放函数,且当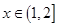 时,
时,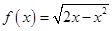 ,求证:函数
,求证:函数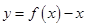 在
在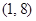 上无零点;
上无零点;
(3)已知函数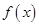 为
为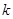 阶缩放函数,且当
阶缩放函数,且当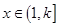 时,
时,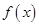 的取值范围是
的取值范围是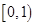 ,求
,求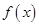 在
在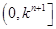 (
(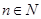 )上的取值范围.
)上的取值范围.
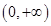 上的函数
上的函数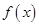 ,如果对任意
,如果对任意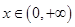 ,恒有
,恒有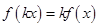 (
(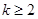 ,
,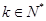 )成立,则称
)成立,则称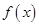 为
为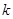 阶缩放函数.
阶缩放函数.(1)已知函数
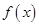 为二阶缩放函数,且当
为二阶缩放函数,且当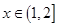 时,
时,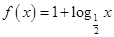 ,求
,求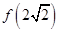 的值;
的值;(2)已知函数
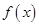 为二阶缩放函数,且当
为二阶缩放函数,且当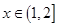 时,
时,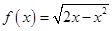 ,求证:函数
,求证:函数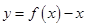 在
在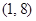 上无零点;
上无零点;(3)已知函数
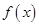 为
为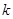 阶缩放函数,且当
阶缩放函数,且当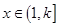 时,
时,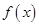 的取值范围是
的取值范围是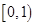 ,求
,求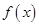 在
在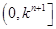 (
(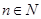 )上的取值范围.
)上的取值范围.(1)1;(2)详见解析;(3)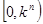 .
.
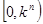 .
.试题分析:(1)本小题首先利用函数
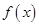 为二阶缩放函数,所以
为二阶缩放函数,所以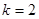 ,于是由
,于是由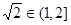 得,
得,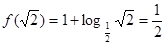 ,由题中条件得
,由题中条件得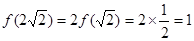 ;
;(2)本小题首先对
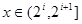
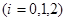 时,
时,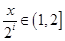 ,得到
,得到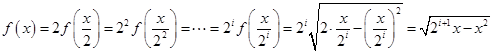 ,方程
,方程
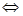
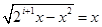
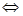
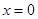 或
或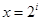 ,
, 与
与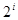 均不属于
均不属于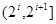 (
(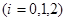 ),所以当
),所以当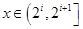
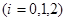 时,方程
时,方程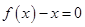 无实数解,所以函数
无实数解,所以函数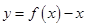 在
在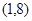 上无零点;
上无零点;(3)本小题针对
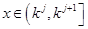 ,
,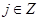 时,有
时,有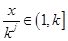 ,依题意可得
,依题意可得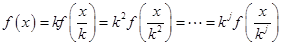 ,然后通过分析可得取值范围为
,然后通过分析可得取值范围为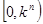 .
.试题解析:(1)由
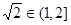 得,
得,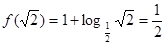 2分
2分由题中条件得
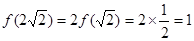 4分
4分(2)当
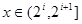
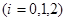 时,
时,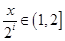 ,依题意可得:
,依题意可得: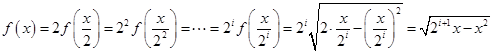 。 6分
。 6分方程

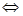
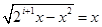
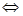
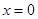 或
或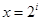 ,
,  与
与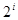 均不属于
均不属于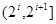 (
(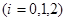 ) 8分
) 8分当
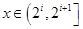 (
(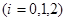 )时,方程
)时,方程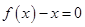 无实数解。
无实数解。注意到
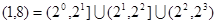 ,所以函数
,所以函数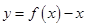 在
在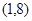 上无零点。 10分
上无零点。 10分(3)当
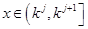 ,
,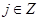 时,有
时,有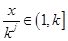 ,依题意可得:
,依题意可得: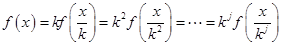
当
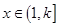 时,
时,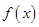 的取值范围是
的取值范围是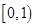 12分
12分所以当
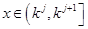 ,
,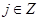 时,
时,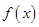 的取值范围是
的取值范围是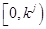 。 14分
。 14分由于
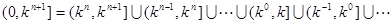 16分
16分所以函数
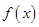 在
在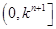 (
(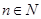 )上的取值范围是:
)上的取值范围是: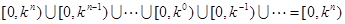 。 18分
。 18分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在
在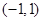 上是减函数,且为奇函数,满足
上是减函数,且为奇函数,满足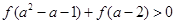 ,试
,试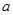 求的范围.
求的范围.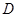 上的函数
上的函数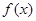 ,若存在闭区间
,若存在闭区间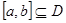 和常数
和常数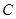 ,使得对任意的
,使得对任意的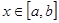 ,都有
,都有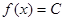 ,且对任意的
,且对任意的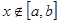 都有
都有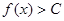 恒成立,则称函数
恒成立,则称函数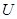 型”函数.
型”函数.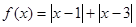 是
是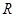 上的“
上的“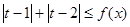 对一切的
对一切的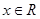 恒成立,求实数
恒成立,求实数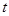 的取值范围;
的取值范围;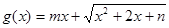 是区间
是区间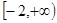 上的“
上的“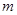 和
和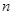 的值.
的值. 与
与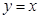 交于
交于 两点且
两点且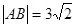 ,奇函数
,奇函数 ,当
,当 时,
时, 与
与 都在
都在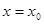 取到最小值.
取到最小值. 的解析式;
的解析式; 图象恰有两个不同的交点,求实数
图象恰有两个不同的交点,求实数 的取值范围.
的取值范围. ,
, ,
, ,则( )
,则( )



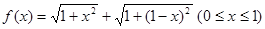 的性质,构造了如图所示的两个边长为
的性质,构造了如图所示的两个边长为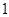 的正方形
的正方形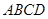 和
和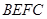 ,点
,点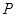 是边
是边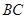 上的一个动点,设
上的一个动点,设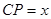 ,则
,则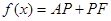 .那么可推知方程
.那么可推知方程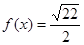 解的个数是( )
解的个数是( )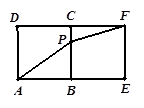
 .
.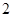 .
.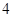 .
.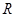 上的奇函数
上的奇函数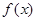 ,
,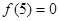 ,且对任意不等的正实数
,且对任意不等的正实数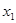 ,
,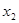 都满足
都满足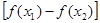
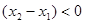 ,则不等式
,则不等式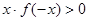 的解集为( ).
的解集为( ). 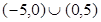



 的图象 ( )
的图象 ( ) ,扇形的周长为定值c,则这个扇形的最大面积为___.
,扇形的周长为定值c,则这个扇形的最大面积为___.