题目内容
已知f(x)=m-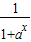 (a>0且a≠1,x∈R)满足f(-x)=-f(x)
(a>0且a≠1,x∈R)满足f(-x)=-f(x)(1)求m的值;
(2)当a=2时,求f(1)的值,并解不等式0<f(x2-x-2)
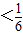
(3)沿着射线y=-x(x≥0)的方向将f(x)的图象平移
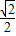 个单位,得到g(x)的图象,求g(x)并求g(-2)+g(-1)+g(0)+g(1)+g(2)+g(3)的值.
个单位,得到g(x)的图象,求g(x)并求g(-2)+g(-1)+g(0)+g(1)+g(2)+g(3)的值.
【答案】分析:(1)利用函数是奇函数的条件进行求值.(2)利用函数的单调性解不等式.(3)利用条件得到一个关系式,利用关系式进行求值.
解答:解:(1)因为f(-x)=-f(x),所以函数为奇函数,所以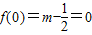 ,解得m=
,解得m= .
.
(2)当a=2时,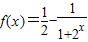 ,所以
,所以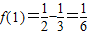 .
.
根据指数函数的性质可知函数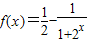 ,在R上单调递增.
,在R上单调递增.
所以由0<f(x2-x-2)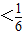 ,得0<f(x2-x-2)<f(1),
,得0<f(x2-x-2)<f(1),
即0<x2-x-2<1,
解得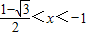 或
或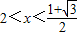 ,
,
所以不等式的解集为得{x|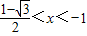 或
或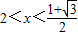 }.
}.
(3)根据题意可知g(x)=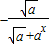 ,并且满足g(x)+g(1-x)=-1,
,并且满足g(x)+g(1-x)=-1,
所以g(-2)+g(-1)+g(0)+g(1)+g(2)+g(3)=-3.
点评:本题主要考查函数奇偶性的应用以及函数单调性的应用,考查学生的运算能力.
解答:解:(1)因为f(-x)=-f(x),所以函数为奇函数,所以
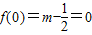 ,解得m=
,解得m= .
.(2)当a=2时,
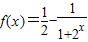 ,所以
,所以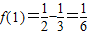 .
.根据指数函数的性质可知函数
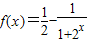 ,在R上单调递增.
,在R上单调递增.所以由0<f(x2-x-2)
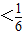 ,得0<f(x2-x-2)<f(1),
,得0<f(x2-x-2)<f(1),即0<x2-x-2<1,
解得
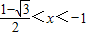 或
或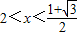 ,
,所以不等式的解集为得{x|
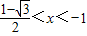 或
或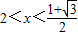 }.
}.(3)根据题意可知g(x)=
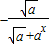 ,并且满足g(x)+g(1-x)=-1,
,并且满足g(x)+g(1-x)=-1,所以g(-2)+g(-1)+g(0)+g(1)+g(2)+g(3)=-3.
点评:本题主要考查函数奇偶性的应用以及函数单调性的应用,考查学生的运算能力.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目