题目内容
如图2-21,过⊙O外一点P作⊙O的两条切线PA、PB,切点分别为A、B,连结AB,在AB、PB、PA上分别取一点D、E、F,使AD =BE,BD =AF,连结DE、DF、EF,则∠EDF与∠P的关系是 .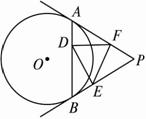
图2-21
思路解析:考虑切线长定理得PA =PB,由条件容易证明△ADF≌△BED,从而∠ADF =∠BED,∠EDF =180°-(∠ADF +∠BDE)=180°-(∠BED+∠BDE )=180°-(180°-∠EBD)=∠EBD =90°-![]() ∠P.
∠P.
答案:∠EDF =90°-![]() ∠P
∠P

练习册系列答案
相关题目
 的椭圆
的椭圆 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。
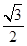 的椭圆
的椭圆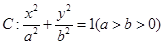 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线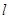 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。 面积的最大值;
面积的最大值;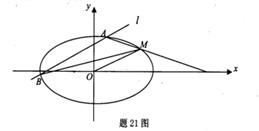

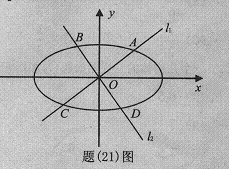 (II)如题(21)图,过坐标原点O且互相垂直的两条直线
(II)如题(21)图,过坐标原点O且互相垂直的两条直线