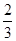题目内容
若两个非零向量
，
满足|+|=|－|=2||，则向量+与－的夹角为( )
A． | B． | C． | D． |
C
解析试题分析：将题目已知条件|+|=|－|=2||各项平方转化，能得•=0，
，利用夹角余弦公式计算，注意等量代换．
考点：向量的运算.
练习册系列答案
相关题目
下列结论中，正确结论的个数是（ ）
（1）若
，且
，则
（2）
（3）
（4）若
,
,
，
，
则
或
| A．0 | B．1 | C．2 | D．3 |
已知直线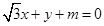
与圆
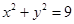交于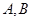
两点，则与向量
(
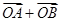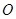为坐标原点)共线的一个向量为（ ）
A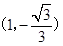． | B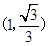． | C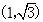． | D． |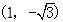
设a、b为不共线的非零向量，
，
，
，那么
为( )
A． |
B． |
C． |
D． |
·
=-1,则|
|的最小值是( )
在△ABC中，N是AC边上一点，且
＝
，P是BN上的一点，若
＝m
＋
，则实数m的值为( )
A． | B． | C．1 | D．3 |
已知向量a、b的夹角为45°，且|a|＝1，|2a－b|＝
，则|b|＝( )
A．3 | B．2 | C． | D．1 |
如图，△ABC中，∠A＝60°，∠A的平分线交BC于D，若AB＝4，且
＝
＋λ
(λ∈R)，则AD的长为( )
A．2 | B．3 | C．4 | D．5 |
已知a,b是不共线的向量,
=λa+b,
=a+μb(λ,μ∈R),那么A,B,C三点共线的充要条件是( )
| A．λ+μ=2 | B．λ-μ=1 |
| C．λμ=-1 | D．λμ=1 |