题目内容
等差数列 中,
中,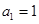 ,
,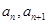 是方程
是方程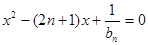 的两个根,则数列
的两个根,则数列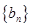 前
前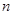 项和
项和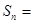 ( )
( )
A.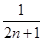 | B.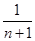 | C.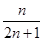 | D.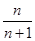 |
D
解析试题分析:因为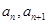 是方程
是方程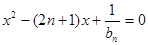 的两个根,所以
的两个根,所以 ,又因为数列
,又因为数列 为等差数列,所以
为等差数列,所以 所以
所以 所以
所以 所以
所以 ,所以
,所以 所以数列
所以数列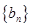 前
前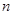 项和
项和
考点:本小题考查通项公式的求法及裂项相消法求数列的前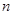 项和.
项和.
点评:对于此类问题,学生应该掌握求通项公式的几种方法和求数列前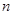 项和的方法等,准确分清该用哪种方法,并且在计算过程中要找清除项数,不要增加也不要减少.
项和的方法等,准确分清该用哪种方法,并且在计算过程中要找清除项数,不要增加也不要减少.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
数列 前
前 项和为
项和为 ,若
,若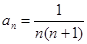 ,则
,则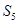 =( )
=( )
A.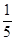 | B.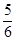 | C.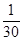 | D.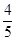 |
数列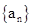 的通项公式为
的通项公式为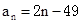 ,当该数列的前
,当该数列的前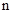 项和
项和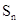 达到最小时,
达到最小时,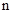 等于( )
等于( )
A.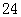 | B.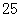 | C.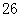 | D.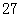 |
数列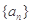 的前n项和
的前n项和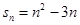 ,则通项公式
,则通项公式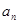 为( )
为( )
A.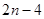 | B.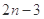 | C.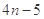 | D.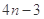 |
数列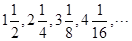 前n项的和为()
前n项的和为()
A.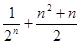 | B.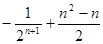 |
C.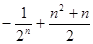 | D.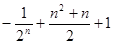 |
等比数列 的前n项和为
的前n项和为 ,若
,若 ( )
( )
| A.3:1 | B.7:3 | C.10:3 | D.2:1 |
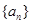 的前
的前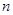 项和
项和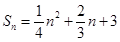 ,则此数列的通项公式为
,则此数列的通项公式为 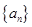 中,
中,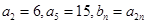 ,则数列
,则数列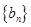 的前5项和
的前5项和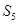 = .
= . ,则该数列前26项的和为________.
,则该数列前26项的和为________.