题目内容
已知数列{an}满足a1=2, .
.
(I)求数列{an}的通项公式;
(II)设bn=(An2+Bn+C)•2n,试推断是否存在常数A,B,C,使对一切n∈N+都有an=bn+1-bn成立?若存在,求出A,B,C的值,若不存在,说明理由.
解:(I)由已知,得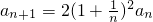 ,
,
即 ,(3分)
,(3分)
所以数列{ }是公比为2的等比数列,首项为a1=2,
}是公比为2的等比数列,首项为a1=2,
故an=2n•n2. (6分)
也可以用累积法;
(II)因为bn+1-bn=[An2+(4A+B)n+2A+2B+C]•2n,
若an=bn+1-bn恒成立,则An2+(4A+B)n+2A+2B+C=n2恒成立,
所以 ,(9分)
,(9分)
解出A=1,B=-4,C=6.
故存在常数A,B,C满足条件. (12分)
分析:(I)由已知,得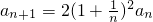 ,所以数列{
,所以数列{ }是公比为2的等比数列,首项为a1=2,由此可知an=2n•n2.
}是公比为2的等比数列,首项为a1=2,由此可知an=2n•n2.
(II)由题题意知若an=bn+1-bn恒成立,则An2+(4A+B)n+2A+2B+C=n2恒成立,由此能解出A=1,B=-4,C=6.故存在常数A,B,C满足条件.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.
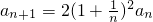 ,
,即
 ,(3分)
,(3分)所以数列{
 }是公比为2的等比数列,首项为a1=2,
}是公比为2的等比数列,首项为a1=2,故an=2n•n2. (6分)
也可以用累积法;
(II)因为bn+1-bn=[An2+(4A+B)n+2A+2B+C]•2n,
若an=bn+1-bn恒成立,则An2+(4A+B)n+2A+2B+C=n2恒成立,
所以
 ,(9分)
,(9分)解出A=1,B=-4,C=6.
故存在常数A,B,C满足条件. (12分)
分析:(I)由已知,得
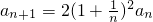 ,所以数列{
,所以数列{ }是公比为2的等比数列,首项为a1=2,由此可知an=2n•n2.
}是公比为2的等比数列,首项为a1=2,由此可知an=2n•n2.(II)由题题意知若an=bn+1-bn恒成立,则An2+(4A+B)n+2A+2B+C=n2恒成立,由此能解出A=1,B=-4,C=6.故存在常数A,B,C满足条件.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目