题目内容
若双曲线x2-y2=1点P（a，b）到直线y=x距离为
+b的值
- A.
- B.
- C.-2
- D.2
B
分析：由题意可得
=
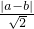，即|a-b|=2，又 a2-b2=1，可得（a+b）（a-b）=1，且a＞b，从而a+b=
=
．
解答：点P（a，b）到直线y=x距离为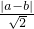，∴=，∴|a-b|=2．
又 a2-b2=1，∴（a+b）（a-b）=1，a＞b，∴a+b===，
故选 B．
点评：本题考查直线和圆锥曲线的位置关系，点到直线的距离公式，得到 （a+b）（a-b）=1，a＞b，是解题的关键．
分析：由题意可得
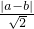=，即|a-b|=2，又 a2-b2=1，可得（a+b）（a-b）=1，且a＞b，从而a+b==．解答：点P（a，b）到直线y=x距离为
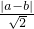，∴=，∴|a-b|=2．又 a2-b2=1，∴（a+b）（a-b）=1，a＞b，∴a+b=
==，故选 B．
点评：本题考查直线和圆锥曲线的位置关系，点到直线的距离公式，得到 （a+b）（a-b）=1，a＞b，是解题的关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
若双曲线x2-y2=1的右支上一点P（a，b）到直线y=x的距离为
，则a+b的值为（ ）
| 2 |
A、-
| ||
B、
| ||
C、±
| ||
| D、±2 |
若双曲线x2-y2=1点P（a，b）到直线y=x距离为
，则a+b的值（ ）
| 2 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |