题目内容
3.已知点 P(-1,1)在曲线y=$\frac{x^2}{x+a}$上,则曲线在点 P处的切线方程为y=-3x-2.分析 代入P的坐标,求得a=2,再求f(x)的导数,求得切线的斜率,由点斜式方程可得切线的方程.
解答 解:点 P(-1,1)在曲线$y=\frac{x^2}{x+a}$上,
可得a-1=1,即a=2,
函数f(x)=$\frac{{x}^{2}}{x+2}$的导数为f′(x)=$\frac{{x}^{2}+4x}{(x+2)^{2}}$,
曲线在点P处的切线斜率为k=-3,
则曲线在点P处的切线方程为y-1=-3(x+1),
即为y=-3x-2.
故答案为:y=-3x-2.
点评 本题考查导数的运用:求切线的方程,注意运用点斜式方程,正确求导是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.下列命题正确的是( )
| A. | 方程$\frac{y}{x-2}=1$表示斜率为1,在y轴上截距为-2的直线 | |
| B. | △ABC的三个顶点是A(-3,0),B(3,0),C(0,3),则中线CO(O为坐标原点)的方程是x=0 | |
| C. | 到y轴距离为2的点的轨迹方程为x=2 | |
| D. | 方程y=$\sqrt{{x}^{2}+2x+1}$表示两条射线 |
 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.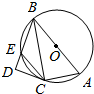 如图,在△ABC中,∠ACB=90°,AB=2AC=8,作△ABC外接圆O的切线CD,作BD⊥CD于D,交圆O于点E,给出下列四个结论:①∠BCD=60°;②DE=2;③BC2=BD•BA;④CE∥AB;则其中正确的序号是①②③④.
如图,在△ABC中,∠ACB=90°,AB=2AC=8,作△ABC外接圆O的切线CD,作BD⊥CD于D,交圆O于点E,给出下列四个结论:①∠BCD=60°;②DE=2;③BC2=BD•BA;④CE∥AB;则其中正确的序号是①②③④.