题目内容

精英家教网棱长为a的正方体ABCD-A1B1C1D1的8个顶点都在球O的表面上，E、F分别是棱AA1、DD1的中点，则直线EF被球O截得的线段长为
 
．
分析：先求球的半径，再求弦长图中QR即可．
解答：解：因为正方体内接于球，所以2R=
a2+a2+a2
，R=
3
2
a，
过球心O和点E、F的大圆的截面图如图所示，
则直线被球截得的线段为QR，过点O作OP⊥QR
于点P，所以，在△QPO中，QR=2QP=2
(
3
a
2
)2-(
a
2
)2
=
2
a
故答案为：
2
a
点评：本题考查组合体的结构特征，考查空间想象能力，是中档题．
练习册系列答案
相关题目
（1）某工厂准备在仓库的一侧建立一个矩形储料场（如图1），现有50米长的铁丝网，如果用它来围成这个储料场，那么长和宽各是多少时，这个储料场的面积最大？并求出这个最大的面积．
（2）如图2，已知AB、DE是圆O的直径，AC是弦，AC∥DE，求证CE=EB．
（3）如图3所示的棱长为a的正方体中：①求CD1和AB所成的角的度数；②求∠B1BD1的正弦值．
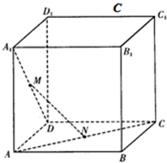精英家教网
精英家教网如图，在棱长为a的正方体ABCD-A1B1C1D1中，M为A1D中点，N为AC中点．
（1）求异面直线MN和AB所成的角；
（2）求点M到平面BB1D1D之距．
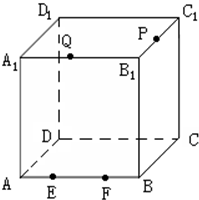精英家教网在棱长为a的正方体ABCD-A1B1C1D1中，P是C1B1的中点，若E，F都是AB上的点，且|EF|=
a2
，Q是A1B1上的点，则四面体EFPQ的体积是
 
．
（2001•上海）在棱长为a的正方体OABC-O′A′B′C′中，E、F分别是棱AB、BC上的动点，且AE=BF．
（Ⅰ）求证：A′F⊥C′E；
（Ⅱ）当三棱锥B′-BEF的体积取得最大值时，求二面角B′-EF-B的大小．（结果用反三角函数表示）
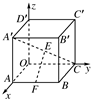如图所示，在空间直角坐标系中，有一棱长为a的正方体ABCO-A′B′C′D′，A′C的中点E与AB的中点F的距离为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网