题目内容
若定义在R上的偶函数f(x)在(-∞,0)上是减函数,且f( )=2.那么不等式f(
)=2.那么不等式f(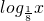 )>2的解集为
)>2的解集为
- A.

- B.

- C.

- D.(2,+∞)
B
分析:本题的函数f(x)是没有给出解析式的抽象函数,用图解法.
解答:根据题意画出函数f(x)的示意图,
不等式f(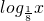 )>2转化为
)>2转化为 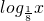 >
> 或
或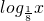 <-
<- ,
,
∴原不等式的解集为 ,
,
故选B.
点评:对于抽象函数的问题,利用图象的直观性,可以化抽象为形象,使问题得以解决,属中档题.
分析:本题的函数f(x)是没有给出解析式的抽象函数,用图解法.
解答:根据题意画出函数f(x)的示意图,
不等式f(
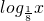 )>2转化为
)>2转化为 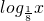 >
> 或
或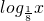 <-
<- ,
,∴原不等式的解集为
 ,
,故选B.
点评:对于抽象函数的问题,利用图象的直观性,可以化抽象为形象,使问题得以解决,属中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
若定义在R上的偶函数f(x)和奇函数g(x)满足f(x)+g(x)=ex,则g(x)=( )
| A、ex-e-x | ||
B、
| ||
C、
| ||
D、
|
若定义在R上的偶函数f(x)在(-∞,0]上是增函数,且f(-
)=2,那么不等式f(sin(2x-
))<2在[-
,
]上的解集为( )
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
A、[-
| ||||||||||||
B、[-
| ||||||||||||
C、[-
| ||||||||||||
D、[-
|
若定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在区间[0,1]上单调递减,则( )
A、f(2)<f(
| ||
B、f(1)<f(2)<f(
| ||
C、f(
| ||
D、f(1)<f(
|