题目内容
已知数列{an}的各项均为正数,前n项和为Sn,且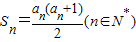
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设
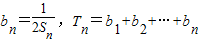 ,求Tn.
,求Tn.
【答案】分析:(Ⅰ)由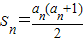 ,知
,知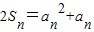 ,
, ,所以(an+an-1)(an-an-1-1)=0,由此能求出an=n.
,所以(an+an-1)(an-an-1-1)=0,由此能求出an=n.
(Ⅱ)由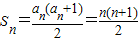 ,知
,知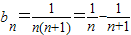 ,由此能求出Tn.
,由此能求出Tn.
解答:解:(Ⅰ)∵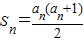 ,
,
∴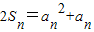 ,①
,①
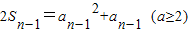 ,②
,②
由①-②得: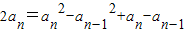 ,(2分)
,(2分)
(an+an-1)(an-an-1-1)=0,
∵an>0,∴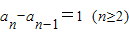 ,
,
又∵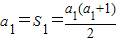 ,
,
∴a1=1,∴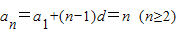 ,(5分)
,(5分)
当n=1时,a1=1,符合题意.
故an=n.(6分)
(Ⅱ)∵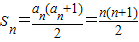 ,
,
∴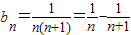 ,(10分)
,(10分)
故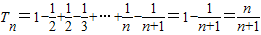 .(12分)
.(12分)
点评:本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,注意迭代法和裂项求和法的合理运用.
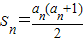 ,知
,知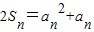 ,
, ,所以(an+an-1)(an-an-1-1)=0,由此能求出an=n.
,所以(an+an-1)(an-an-1-1)=0,由此能求出an=n.(Ⅱ)由
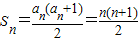 ,知
,知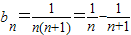 ,由此能求出Tn.
,由此能求出Tn.解答:解:(Ⅰ)∵
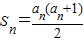 ,
,∴
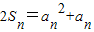 ,①
,①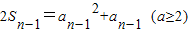 ,②
,②由①-②得:
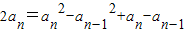 ,(2分)
,(2分) (an+an-1)(an-an-1-1)=0,
∵an>0,∴
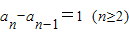 ,
,又∵
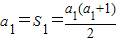 ,
,∴a1=1,∴
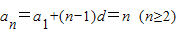 ,(5分)
,(5分)当n=1时,a1=1,符合题意.
故an=n.(6分)
(Ⅱ)∵
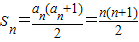 ,
,∴
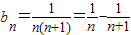 ,(10分)
,(10分)故
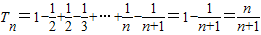 .(12分)
.(12分)点评:本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,注意迭代法和裂项求和法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)
 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)