题目内容
已知点M(0,-1)、F(0,1),过点M的直线l与曲线y=(1)求直线l的方程;
(2)求以点F为焦点,l为准线的抛物线C的方程.
解:(1)因为f′(2)=![]()
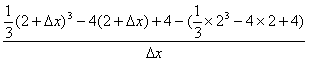 =0,
=0,
所以直线l的斜率为0,其直线方程为y=-1.
(2)因为抛物线以点F(0,1)为焦点,y=-1为准线,设抛物线方程为x2=2py,则![]() =1,p=2.
=1,p=2.
故抛物线C的方程为x2=4y.

练习册系列答案
相关题目
题目内容
已知点M(0,-1)、F(0,1),过点M的直线l与曲线y=(1)求直线l的方程;
(2)求以点F为焦点,l为准线的抛物线C的方程.
解:(1)因为f′(2)=![]()
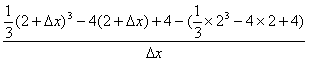 =0,
=0,
所以直线l的斜率为0,其直线方程为y=-1.
(2)因为抛物线以点F(0,1)为焦点,y=-1为准线,设抛物线方程为x2=2py,则![]() =1,p=2.
=1,p=2.
故抛物线C的方程为x2=4y.
