题目内容
如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10 km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.
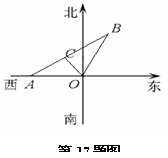
如图,令|OA|=a,|OB|=b,则在△AOB中,∠AOB=120°.…………………………………………2分
∴![]() |OC||AB|=
|OC||AB|=![]() absin120°.
absin120°.
∴|AB|=![]() . ① …………………4分
. ① …………………4分
又由余弦定理,
|AB|=![]() =
=![]()
≥![]() =
=![]() ,(当a=b时取等号.) ② ……………6分
,(当a=b时取等号.) ② ……………6分
由①②知![]() ≥3ab.
≥3ab.
∵ab>0,
∴ab≥400 ③ …………………………………………………8分
③代入①得|AB|=![]() ≥20
≥20![]() .
.
当a=b时|AB|取得最小值.…………………………………………………………10分
而a=b时,△AOB为等腰三角形,
∴∠OAB=∠OBA=30°.
∴a=b=20.
∴A、B两点的最佳位置是距市中心O均为20km处. ……………………………12分

练习册系列答案
相关题目
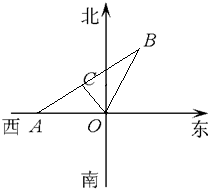 如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.
如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.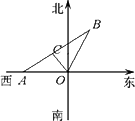
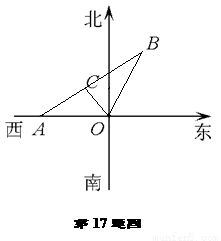
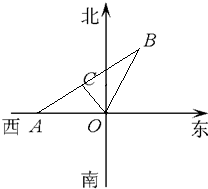 如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.
如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.