题目内容
观察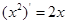 ,
,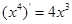 ,
,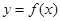 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在 上的函数
上的函数 满足
满足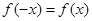 ,记
,记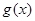 为
为 的导函数,则
的导函数,则 =( )
=( )
A. | B.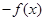 | C.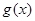 | D.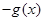 |
D
解析试题分析:∵定义在 上的函数
上的函数 满足
满足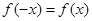 ,∴函数
,∴函数 为偶函数,又根据
为偶函数,又根据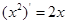 ,
,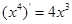 归纳出偶函数的导数为奇函数,故函数g(x)为奇函数,∴
归纳出偶函数的导数为奇函数,故函数g(x)为奇函数,∴ =-g(x),故选D
=-g(x),故选D
考点:本题考查了导数的运用及函数的性质
点评:熟练运用函数的性质求值是解决此类问题的关键,属基础题

练习册系列答案
相关题目
已知点 在曲线
在曲线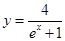 上,
上, 为曲线在点
为曲线在点 处的切线的倾斜角,则
处的切线的倾斜角,则 的取值范围为( )
的取值范围为( )
A.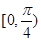 | B.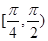 | C. | D.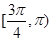 |
函数 =
=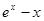 (
(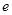
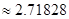 )在区间[-1,1]上的最大值是( )
)在区间[-1,1]上的最大值是( )
A.1+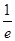 | B.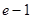 | C.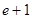 | D.1 |
根据定积分的几何意义,计算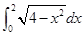 的结果是( )
的结果是( )
A.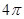 | B.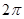 | C.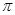 | D.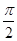 |
曲线f(x)=x㏑x在点x=1处的切线方程是( )
| A.y=2x+2 | B.y=2x-2 | C.y=x-1 | D.y=x+1 |
设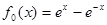 ,且对任意的
,且对任意的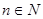 ,都有
,都有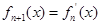 ,则
,则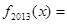
A.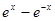 | B.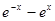 | C.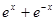 | D.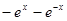 |
若函数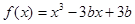 在
在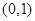 内有极小值,则 ( )
内有极小值,则 ( )
A.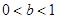 | B.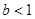 | C.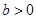 | D.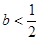 |
函数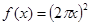 的导数是( )
的导数是( )
A.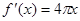 | B.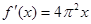 | C.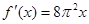 | D.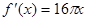 |
过点(0,1)且与曲线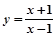 在点(3,2)处的切线垂直的直线的方程为( )
在点(3,2)处的切线垂直的直线的方程为( )
A.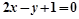 | B.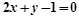 |
C.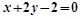 | D.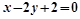 |