题目内容
已知函数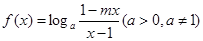 的图象关于原点对称。
的图象关于原点对称。
(1)求m的值;(2)判断 在
在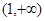 上的单调性,并根据定义证明。
上的单调性,并根据定义证明。
【答案】
(1) ;(2)当
;(2)当 时,
时, ,由函数单调性定义知
,由函数单调性定义知 在
在 上单调增;当
上单调增;当 时,
时,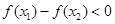 ,由函数单调性定义知
,由函数单调性定义知 在
在 上单调减。
上单调减。
【解析】
试题分析:(1)由已知条件得 ------------2分
------------2分
即 ,
, ,即
,即 ------2分
------2分
当 时,
时, 无意义,故
无意义,故 舍去
舍去
因此,只有 满足题意-----------2分
满足题意-----------2分
(2)由(1)知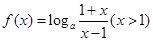 ,设
,设
则
 ,且
,且 ,
, ,
, ------------4分
------------4分
当 时,
时, ,由函数单调性定义知
,由函数单调性定义知 在
在 上单调增
上单调增
当 时,
时,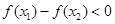 ,由函数单调性定义知
,由函数单调性定义知 在
在 上单调减
上单调减
-----------------3分
考点:函数的奇偶性;函数的单调性;用定义法证明函数的单调性。
点评:用定义法证明函数单调性的步骤:一设二作差三变形四判断符号五得出结论,其中最重要的是四变形,最好变成几个因式乘积的形式,这样便于判断符号。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,∠B=60°,AB=1的△ABC有两个.其中正确命题的代号是_________.(按照原顺序将所有正确命题的代号都写出来)
,∠B=60°,AB=1的△ABC有两个.其中正确命题的代号是_________.(按照原顺序将所有正确命题的代号都写出来) ,给出下列命题:
,给出下列命题:
 ,则f(x)在区间[a,+∞)上是增函数;
,则f(x)在区间[a,+∞)上是增函数; ,其中正确命题的代号是________(按照原顺序将你认为正确的命题的代号都填上).
,其中正确命题的代号是________(按照原顺序将你认为正确的命题的代号都填上).