题目内容
某造船公司年造船量是20艘,已知造船![]() 艘的产值函数为R(x)=3700x+45x2-10x3(单位:万元),成本函数为C(x)=460x+5000(单位:万元),又在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x)。
艘的产值函数为R(x)=3700x+45x2-10x3(单位:万元),成本函数为C(x)=460x+5000(单位:万元),又在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x)。
(Ⅰ)求利润函数P(x)及边际利润函数MP(x);(提示:利润=产值成本)
(Ⅱ)问年造船量安排多少艘时,可使公司造船的年利润最大?
(Ⅲ)求边际利润函数MP(x)单调递减时x的取值范围,并说明单调递减在本题中的实际意义是什么?解析:(Ⅰ)P(x)=R(x)-C(x)=-10x3+45x2+3240x-5000,(x![]() N*,且1≤x≤20); MP(x)=P(x+1)-P(x)=-30x2+60x+3275,(x
N*,且1≤x≤20); MP(x)=P(x+1)-P(x)=-30x2+60x+3275,(x![]() N*,且1≤x≤19)
N*,且1≤x≤19)
(Ⅱ)![]() .
.
∴当0<x<12时![]() >0,当x<12时,
>0,当x<12时,![]() <0.
<0.
∴x=12,P(x)有最大值.
即年造船量安排12 艘时,可使公司造船的年利润最大.
(Ⅲ)∵MP(x)=-30x2+60x+3275=-30(x-1)2+3305,
所以,当x≥1时,MP(x)单调递减,x的取值范围为[1,19],且x![]() N*
N*
![]() 是减函数的实际意义:随着产量的增加,每艘船的利润在减少.
是减函数的实际意义:随着产量的增加,每艘船的利润在减少.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 艘的产值函数为
艘的产值函数为 (单位:万元),成本函数为
(单位:万元),成本函数为 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数 的边际函数
的边际函数 定义为
定义为 。
。 及边际利润函数
及边际利润函数 ;(提示:利润=产值-成本)
;(提示:利润=产值-成本) 艘的产值函数为
艘的产值函数为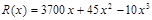 (单位:万元),成本函数为
(单位:万元),成本函数为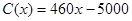 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数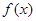 的边际函数
的边际函数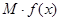 定义为
定义为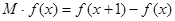 。
。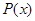 及边际利润函数
及边际利润函数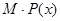 ;(提示:利润=产值-成本)
;(提示:利润=产值-成本)