Question

【题目】如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．
（Ⅰ）证明：SD⊥平面SAB；
（Ⅱ）求AB与平面SBC所成的角的大小．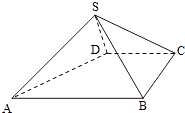

Answer 1

【答案】证明：（Ⅰ）在直角梯形ABCD中，
∵AB∥CD，BC⊥CD，AB=BC=2，CD=1
∴AD= =
∵侧面SAB为等边三角形，AB=2
∴SA=2
∵SD=1
∴AD2=SA2+SD2
∴SD⊥SA
同理：SD⊥SB
∵SA∩SB=S，SA，SB面SAB
∴SD⊥平面SAB
（Ⅱ）建立如图所示的空间坐标系

则A（2，﹣1，0），B（2，1，0），C（0，1，0），
作出S在底面上的投影M，则由四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形知，M点一定在x轴上，又AB=BC=2，CD=SD=1．可解得MD= ，从而解得SM= ，故可得S（ ，0， ）
则
设平面SBC的一个法向量为
则 ，
即
取x=0，y= ，z=1
即平面SBC的一个法向量为 =（0， ，1）
又 =（0，2，0）
cos＜ ， ＞= = =
∴＜ ， ＞=arccos
即AB与平面SBC所成的角的大小为arcsin
【解析】（1）利用线面垂直的判定定理，即证明SD垂直于面SAB中两条相交的直线SA，SB；在证明SD与SA，SB的过程中运用勾股定理即可（Ⅱ）求AB与平面SBC所成的角的大小即利用平面SBC的法向量 ，当 为锐角时，所求的角即为它的余角；当 为钝角时，所求的角为
【考点精析】通过灵活运用直线与平面垂直的判定和空间角的异面直线所成的角，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则即可以解答此题．