题目内容
已知⊙C经过点A（2，4）、B（3，5）两点，且圆心C在直线2x-y-2=0上．则⊙C的方程是 ．
【答案】分析：根据圆的性质，算出AB的垂直平分线y=-x+2，与直线2x-y-2=0联解得出C（3，4），求出圆的C的半径r=1，从而可得⊙C的方程．
解答：解：∵⊙C经过点A（2，4）、B（3，5）两点，
∴点C在线段AB的垂直平分线y=-x+2
又∵圆心C在直线2x-y-2=0上
∴联解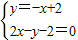
，得C（3，4）
圆C的半径r=|AC|=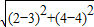
=1
∴⊙C的方程是（x-3）2+（y-4）2=1
故答案为：（x-3）2+（y-4）2=1
点评：本题给出经过A、B两点的圆的圆心在已知直线上，求圆的方程．着重考查了圆的方程、直线与圆的位置关系等知识，属于基础题．
解答：解：∵⊙C经过点A（2，4）、B（3，5）两点，
∴点C在线段AB的垂直平分线y=-x+2
又∵圆心C在直线2x-y-2=0上
∴联解
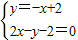，得C（3，4）圆C的半径r=|AC|=
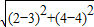=1∴⊙C的方程是（x-3）2+（y-4）2=1
故答案为：（x-3）2+（y-4）2=1
点评：本题给出经过A、B两点的圆的圆心在已知直线上，求圆的方程．着重考查了圆的方程、直线与圆的位置关系等知识，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目