题目内容
(本小题满分12分)
已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() 、
、![]() ,短轴两个端点为
,短轴两个端点为![]() 、
、![]() ,
,
且四边形![]() 是边长为2的正方形。
是边长为2的正方形。
(1)求椭圆方程;
(2)若![]() 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点![]() 满足
满足![]() ,连接
,连接![]() ,交椭圆于点
,交椭圆于点![]() ;
;
证明:![]() 为定值;
为定值;
(3)在(2)的条件下,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的定点
的定点![]() ,使得以
,使得以![]() 为直径的圆恒
为直径的圆恒
过直线![]() 的交点,若存在,求出点
的交点,若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
解:(1)![]() ,
,![]() ,
,![]() 椭圆方程为
椭圆方程为![]() 。…2分
。…2分
(2)![]() ,设
,设![]() ,则
,则![]() 。
。
直线![]() :
:![]() ,即
,即![]() ,……………………………4分
,……………………………4分
代入椭圆![]() 得
得![]() 。…………5分
。…………5分
![]() ,
,![]() 。
。![]() ,…7分
,…7分
![]()
![]() (定值)。…………8分
(定值)。…………8分
(3)设存在![]() 满足条件,则
满足条件,则![]() 。
。
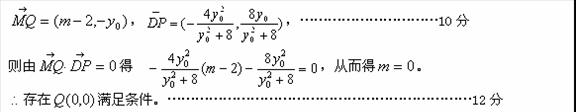

练习册系列答案
相关题目