题目内容
已知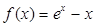 ,
,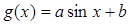 ,
,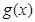 在
在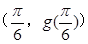 处的切线方程为
处的切线方程为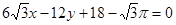
(Ⅰ)求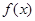 的单调区间与极值;
的单调区间与极值;
(Ⅱ)求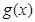 的解析式;
的解析式;
(III)当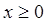 时,
时,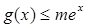 恒成立,求
恒成立,求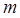 的取值范围.
的取值范围.
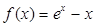 ,
,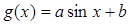 ,
,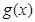 在
在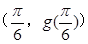 处的切线方程为
处的切线方程为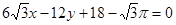
(Ⅰ)求
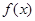 的单调区间与极值;
的单调区间与极值;(Ⅱ)求
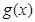 的解析式;
的解析式;(III)当
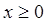 时,
时,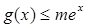 恒成立,求
恒成立,求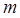 的取值范围.
的取值范围.(Ⅰ)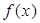 的增区间为
的增区间为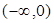 ,减区间为
,减区间为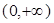 ,
,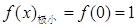 ;
;
(Ⅱ)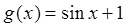 ;(III)
;(III)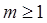 .
.
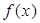 的增区间为
的增区间为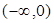 ,减区间为
,减区间为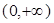 ,
,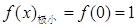 ;
;(Ⅱ)
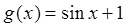 ;(III)
;(III)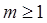 .
.试题分析:(Ⅰ)令
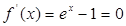 ,得
,得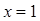 , 1分
, 1分∴当
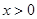 时,
时,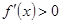 ;当
;当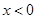 时,
时,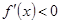 。
。∴
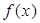 的增区间为
的增区间为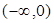 ,减区间为
,减区间为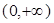 ,
,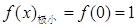 , 3分
, 3分(Ⅱ)
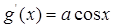 ,
,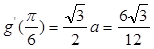 ,所以
,所以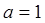 。
。又
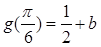
∴
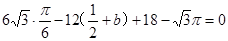 ,∴
,∴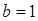
所以
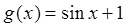 6分
6分(III)当
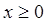 时,
时,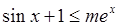 ,令
,令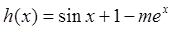
当
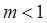 时,
时,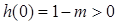 矛盾, 8分
矛盾, 8分首先证明
 在
在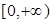 恒成立.
恒成立.令
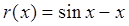 ,
,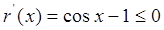 ,故
,故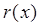 为
为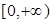 上的减函数,
上的减函数,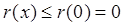 ,故
,故 10分
10分由(Ⅰ)可知
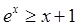 故 当
故 当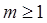 时,
时,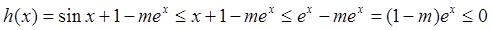
综上
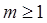 12分
12分点评:难题,不等式恒成立问题,常常转化成求函数的最值问题。不等式恒成立问题,往往要通过构造函数,研究函数的单调性、极值(最值),进一步确定得到参数的范围。

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
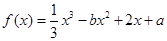 ,
,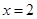 是
是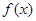 的一个极值点.
的一个极值点.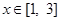 时,
时,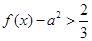 恒成立,求实数
恒成立,求实数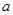 的取值范围.
的取值范围.
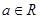
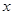 的不等式
的不等式 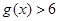
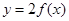 的图象恒在函数
的图象恒在函数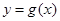 的上方,求实数
的上方,求实数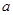 的取值范围。
的取值范围。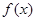 在定义域
在定义域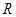 内可导,若
内可导,若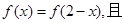
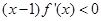 ,若
,若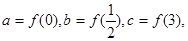 则
则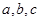 的大小关系是( )
的大小关系是( ) 
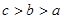
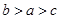

 的有铝合金盖的圆柱形铁桶,已知单位面积铝合金的价格是铁的3倍,问底面半径多大时桶的总造价最小?
的有铝合金盖的圆柱形铁桶,已知单位面积铝合金的价格是铁的3倍,问底面半径多大时桶的总造价最小?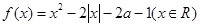 有四个不同的零点,则实数
有四个不同的零点,则实数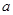 的取值范围是_______________.
的取值范围是_______________.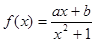 在
在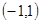 上是增函数,且
上是增函数,且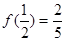
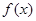 的解析式;
的解析式;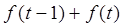 <0.
<0.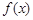 对任意
对任意 都有
都有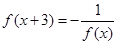 ,且当
,且当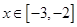 时,
时, ,则
,则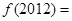 .
.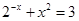 的实数解的个数为1;
的实数解的个数为1; 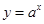 的图象可以由函数
的图象可以由函数 (其中
(其中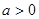 且
且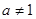 )平移得到;
)平移得到;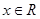 ,有
,有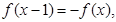 则
则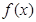 的周期为2;
的周期为2;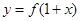 与函数
与函数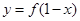 的图象关于直线
的图象关于直线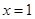 对称.
对称.