题目内容
已知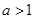 ,若函数
,若函数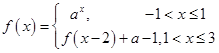 ,则
,则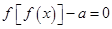 的
的
根的个数最多有
| A.1个 | B.2个 | C.3个 | D.4个 |
C
解析本题考查分段函数和复合函数的知识。可以用数形结合的方法解决。可以把所求的复合函数从里向外打开,再由外向里求解。
如图,粗略画出函数的图像。先计算外层,从两段函数图像上找到纵坐标为 的点。得到点
的点。得到点 .。
.。
此时有 。
。
再计算内层,分别作直线 ,改变参数
,改变参数 。它们与原函数最多有
。它们与原函数最多有 个交点,故最多有
个交点,故最多有 个解。
个解。
本题体现了数形结合的思想方法,求解复合函数的时候,解方程由外向里,求值计算由里向外。

练习册系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,其最小正周期为3,且x∈(-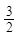 ,0)时,f(x)=log2(-3x+1),则f(2011)=( )
,0)时,f(x)=log2(-3x+1),则f(2011)=( )
| A.4 | B.2 | C.-2 | D.log27 |
下列四个函数中,在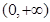 上为增函数的是 ( )
上为增函数的是 ( )
A.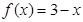 | B.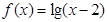 |
C.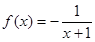 | D.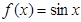 |
如果奇函数 在区间
在区间 上是增函数,且最小值为
上是增函数,且最小值为 ,那么
,那么 在区间
在区间 上是
上是
A.增函数且最小值为 | B.增函数且最大值为 |
C.减函数且最小值为 | D.减函数且最大值为 |
“函数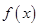 在
在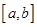 上单调”是“函数
上单调”是“函数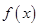 在
在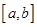 上有最大值和最小值”的( )条件.
上有最大值和最小值”的( )条件.
| A.充分但不必要 | B.必要但不充分 |
| C.充分必要 | D.既不充分也不必要 |
若函数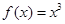 (
(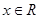 ),则函数
),则函数 在其定义域上是
在其定义域上是
| A.单调递减的偶函数 | B.单调递减的奇函数 |
| C.单凋递增的偶函数 | D.单调递增的奇函数 |
定义在R上的函数f(x)满足f(x)= 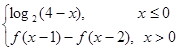 ,则f(3)的值
,则f(3)的值
为( )
| A.-1 | B.-2 | C.1 | D.2 |
若函数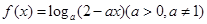 在区间
在区间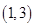 内单调递增,则
内单调递增,则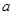 的取值范围是
的取值范围是
A.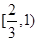 | B.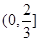 | C.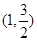 | D.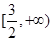 |
 的定义域是( )
的定义域是( ) .(4,+∞) D.[4,+∞)
.(4,+∞) D.[4,+∞)