题目内容
已知函数f(x)=a•bx的图象过点 .
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)记an=log2f(n),n是正整数,Sn是数列{an}的前n项的和,求S30.
解:(Ⅰ)∵函数f(x)=a•bx的图象过点 .
.
∴可得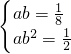 (2分) 解得
(2分) 解得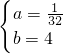 (4分)
(4分)
∴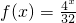 (5分)
(5分)
(Ⅱ)由题意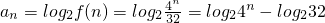 =2n-5,n∈N*(7分)
=2n-5,n∈N*(7分)
因为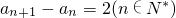 故{an}是等差数列,且a1=-3,(9分)
故{an}是等差数列,且a1=-3,(9分)
由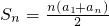 ,得
,得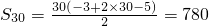 .
.
故答案为:780.(12分)
分析:(Ⅰ)函数f(x)=a•bx的图象过点 ,则必有
,则必有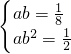 解出ab的值即可写出解析式;
解出ab的值即可写出解析式;
(Ⅱ)由(1)知: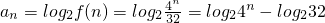 =2n-5,可证{an}是等差数列,代入前n项和公式即得.
=2n-5,可证{an}是等差数列,代入前n项和公式即得.
点评:本题为等差数列的求和问题,涉及指数函数,由函数构造数列并证明为等差数列是解决问题的关键,属中档题.
 .
.∴可得
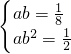 (2分) 解得
(2分) 解得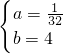 (4分)
(4分)∴
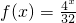 (5分)
(5分)(Ⅱ)由题意
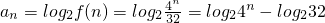 =2n-5,n∈N*(7分)
=2n-5,n∈N*(7分)因为
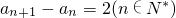 故{an}是等差数列,且a1=-3,(9分)
故{an}是等差数列,且a1=-3,(9分)由
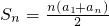 ,得
,得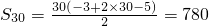 .
.故答案为:780.(12分)
分析:(Ⅰ)函数f(x)=a•bx的图象过点
 ,则必有
,则必有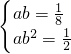 解出ab的值即可写出解析式;
解出ab的值即可写出解析式;(Ⅱ)由(1)知:
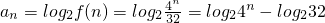 =2n-5,可证{an}是等差数列,代入前n项和公式即得.
=2n-5,可证{an}是等差数列,代入前n项和公式即得.点评:本题为等差数列的求和问题,涉及指数函数,由函数构造数列并证明为等差数列是解决问题的关键,属中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目