Question

在三棱锥P-ABC中，AB⊥BC，AB=BC，PA=2BC，点O是AC的中点，OP⊥底面ABC．求直线PA与平面PBC所成角的大小．

Answer 1

分析：取PC中点D，欲求直线PA与平面PBC所成角可转化成求直线OD与平面PBC所成的角，取BC的中点E，连接PE，过点O作PE⊥OH，
根据线面所成角可知∠ODH为直线PA与平面PBC所成角，在三角形ODH中求出此角即可．

解答：解：取PC中点D，PA∥OD，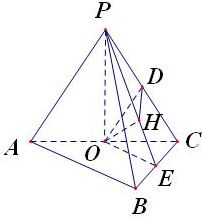
欲求直线PA与平面PBC所成角可转化成求直线OD与平面PBC所成的角，
取BC的中点E，连接PE，过点O作PE⊥OH，
∴∠ODH为直线PA与平面PBC所成角
设AB=BC=1，PA=2，OD=1
OE=

1

2

，PO=

6

2

，OH=

210

30

∴∠ODH=arcsin

210

30

．

点评：本题主要考查了直线与平面所成的角，以及转化的数学思想，属于中档题．