题目内容
（本题满分１２分）
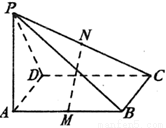
如图，已知
内接于圆
，
是圆的直径，四边形
为平行四边形，
平面
，
，
。
⑴证明: DE⊥平面ADC；
⑵记
求三棱锥
的体积
；
⑶当取得最大值时，求证：
。
【答案】
⑴见解析；⑵
(
；⑶
。
【解析】本试题主要是考查了立体几何中的线面的垂直问题以及锥体的体积公式，以及取得最值时边长关系的证明。
（1）
内接于圆
，
是圆的直径
平面
平面
四边形
为平行四边形
平面
（2）因为
，
(
(
（3）
(
，利用均值不等式得到最值成立的条件。
⑴内接于圆，是圆的直径
平面
平面
四边形为平行四边形
平面
⑵，
(
(
⑶(
当且仅当
时等号成立
此时
，
。
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
相关题目
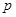与死亡年数
之间的函数关系式；
）
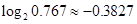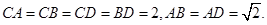
平面BCD；
