题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() ,点
,点![]() ,
,![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(1)求![]() 的最小值及相应点
的最小值及相应点![]() 的坐标;
的坐标;
(2)点![]() 到直线
到直线![]() 距离的最小值及相应点
距离的最小值及相应点![]() 的坐标;
的坐标;
(3)直线![]() 过点
过点![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,交直线
两点,交直线![]() 于
于![]() 点,若
点,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)3,![]() ;(2)
;(2)![]() ,
,![]() ;(3)0.
;(3)0.
【解析】
(1)根据抛物线的定义转换线段关系求解即可.
(2)设![]() 再求出点到线的距离公式分析最值即可.
再求出点到线的距离公式分析最值即可.
(3)设直线![]() 方程为
方程为![]() ,再联立直线
,再联立直线![]() 与抛物线和
与抛物线和![]() ,分别表示出
,分别表示出![]() 的坐标,再根据
的坐标,再根据![]() ,
,![]() 表达出
表达出![]() 再代入韦达定理化简即可.
再代入韦达定理化简即可.
(1) 作![]() 垂直于准线于
垂直于准线于![]() ,则
,则![]() ,由图易得当直线
,由图易得当直线![]() 轴时
轴时![]() 取得最小值
取得最小值![]() ,此时
,此时![]() 与
与![]() 横坐标相同,此时
横坐标相同,此时![]() .
.
即当![]() 时
时![]() 取得最小值3.
取得最小值3.
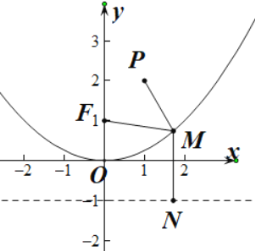
(2) 设![]() 则点
则点![]() 到直线
到直线![]() 距离
距离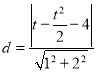
![]() .当
.当![]() 时取最小值
时取最小值![]() .
.
故当![]() 时
时![]() 到直线
到直线![]() 距离的最小值取
距离的最小值取![]() .
.
(3)显然直线![]() 有斜率,设直线
有斜率,设直线![]() 方程为
方程为![]() .
.![]() .
.
联立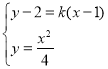
![]() .则
.则![]() .
.
![]() .
.
又![]() ,故
,故![]() ,故
,故![]() ,
,
![]() ,故
,故![]() ,故
,故![]() .
.
所以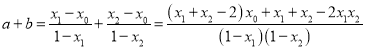 .
.
又![]()
![]() .故
.故![]()


练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
【题目】在第十五次全国国民阅读调查中,某地区调查组获得一个容量为![]() 的样本,其中城镇居民
的样本,其中城镇居民![]() 人,农村居民
人,农村居民![]() 人.在这些居民中,经常阅读的城镇居民
人.在这些居民中,经常阅读的城镇居民![]() 人,农村居民
人,农村居民![]() 人.
人.
(1)填写下面列联表,并判断是否有![]() 的把握认为,经常阅读与居民居住地有关?
的把握认为,经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 |
|
| |
不经常阅读 | |||
合计 |
|
(2)调查组从该样本的城镇居民中按分层抽样抽取出![]() 人,参加一次阅读交流活动,若活动主办方从这
人,参加一次阅读交流活动,若活动主办方从这![]() 位居民中随机选取
位居民中随机选取![]() 人作交流发言,求被选中的
人作交流发言,求被选中的![]() 位居民都是经常阅读居民的概率.
位居民都是经常阅读居民的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|