题目内容
随机变量ξ服从正态分布N(1,4),若P(2<ξ<3)=a,则P(ξ<-1)+P(1<ξ<2)=( )
分析:根据变量符合正态分布,知道正态曲线关于x+1对称,根据对称点特点,写出对称轴两侧的对称区间的概率之间的关系,写出要求的区间的概率值.
解答:解:∵随机变量ξ服从正态分布N(1,4),
∴正态曲线关于x=1对称,
∵P(2<ξ<3)=a,
∴P(-1<ξ<0)=a,P(1<ξ<2)=P(0<ξ<1)
P(ξ<-1)+P(1<ξ<2)=
-a,
故选B.
∴正态曲线关于x=1对称,
∵P(2<ξ<3)=a,
∴P(-1<ξ<0)=a,P(1<ξ<2)=P(0<ξ<1)
P(ξ<-1)+P(1<ξ<2)=
| 1 |
| 2 |
故选B.
点评:本题考查正态分布曲线的特点及曲线所表示的意义,考查正态曲线的对称性,考查对称区间概率之间的关系,本题是一个基础题.

练习册系列答案
相关题目
 服从正态分 布
服从正态分 布 ,若
,若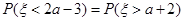 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 ,则ξ的期望和标准差分别是( )
,则ξ的期望和标准差分别是( )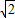
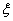 服从正态分布,其概率密度函数为
服从正态分布,其概率密度函数为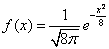 ,则
,则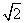 D.0和2
D.0和2