Question

素材1：y=f(x)为（0，+∞）上的增函数；

素材2：f(x)+f(x-)≤0;

素材3：函数y=f(x)（x∈R且x≠0）对任意非零实数x₁、x₂，恒有f(x₁x₂)=f(x₁)+f(x₂).

先将上面的素材构建成一个问题，然后再解答.

Answer 1

构建问题：设函数y=f(x)(x∈R且x≠0）对任意非零实数x₁、x₂，恒有f(x₁x₂)=f(x₁)+f(x₂)，

（1）求证：y=f(x)是偶函数；

（2）已知y=f(x)为(0,+∞)上的增函数，求适合f(x)+f(x-)≤0的x的取值范围.

（1）证明：∵f(x₁x₂)=f(x₁)+f(x₂)(x₁x₂≠0),

∴f(1)=f(1)+f(1)=2f(1).

∴f(1)=0.

∴f(1)=f(-1)+f(-1)=2f(-1).

∴2f(-1)=0，即f(-1)=0.

对任意的x≠0,都有f(-x)=f(-1)+f(x)=f(x),

∴f(x)为偶函数.

（2）解析：∵f(x₁x₂)=f(x₁)+f(x₂)(x₁x₂≠0),

∴f(x)+f(x-)=f(x²-x).

∵f(x)+f(x-)≤0,

∴f(x²-x)≤0.

∵f(x)为偶函数且f(1)=0,

∴f(|x²-x|)≤f(1).

∵f(x)在（0，+∞）上是增函数,

∴

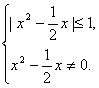
∴≤x≤且x≠0,x≠.