题目内容
已知数列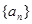 ,
,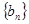 满足:
满足: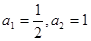 ,
,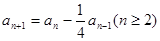 ;
;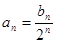 (
(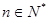 )
)
(Ⅰ)计算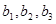 ,并求数列
,并求数列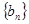 ,
,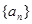 的通项公式;
的通项公式;
(Ⅱ)证明:对于任意的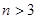 ,都有
,都有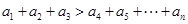 .
.
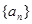 ,
,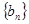 满足:
满足: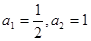 ,
,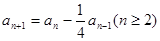 ;
;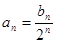 (
(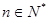 )
)(Ⅰ)计算
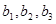 ,并求数列
,并求数列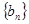 ,
,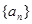 的通项公式;
的通项公式;(Ⅱ)证明:对于任意的
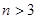 ,都有
,都有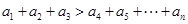 .
.(Ⅰ) ………………………………………
……………………………………… 分
分
将 ,
, ,
, 代入
代入 中化简得:
中化简得:  可见,数列
可见,数列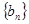 是等差数列. …………………………………………
是等差数列. ………………………………………… 分
分
由 知其公差为3,故
知其公差为3,故 …………………………………………………………………………………
………………………………………………………………………………… 分
分
 . …………………………………………………………
. ………………………………………………………… 分
分
(Ⅱ)设数列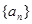 的前
的前 项和为
项和为 则
则
 ,
,
 ,……………………………
,…………………………… 分
分
相减可得:

 ,………………………………………………
,……………………………………………… 分
分
可见,对于任意的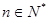 ,总有
,总有 但
但 ,
, 故当
故当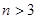 时
时

 ………………………………………
……………………………………… 分
分将
 ,
, ,
, 代入
代入 中化简得:
中化简得:  可见,数列
可见,数列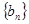 是等差数列. …………………………………………
是等差数列. ………………………………………… 分
分由
 知其公差为3,故
知其公差为3,故 …………………………………………………………………………………
………………………………………………………………………………… 分
分 . …………………………………………………………
. ………………………………………………………… 分
分(Ⅱ)设数列
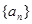 的前
的前 项和为
项和为 则
则 ,
, ,……………………………
,…………………………… 分
分相减可得:

 ,………………………………………………
,……………………………………………… 分
分可见,对于任意的
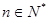 ,总有
,总有 但
但 ,
, 故当
故当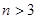 时
时
略

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 中,
中, ,公差
,公差 ,则使前
,则使前 项和
项和 取最大的正整数
取最大的正整数 为等差数列,其公差为-2,且
为等差数列,其公差为-2,且 是
是 与
与 的等比中项,
的等比中项, 为
为 , 则
, 则 的值为( )
的值为( )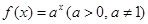 的图象上一点,数列
的图象上一点,数列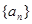 的前
的前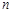 项和是
项和是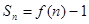 .
.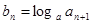 ,求数列
,求数列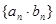 的前
的前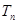
 中,
中, 则
则 ( )
( ) 的前
的前 项和是
项和是 ,若
,若 则
则 的值为( )
的值为( )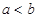 ,且
,且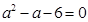 ,
,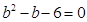 ,数列
,数列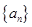 、
、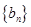 满足
满足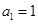 ,
,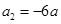 ,
,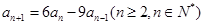 ,
,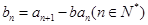 .
.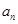 ;
;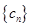 满足
满足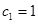 ,
,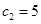 ,
,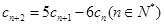 ,试用数学归纳法证明:
,试用数学归纳法证明: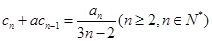 .
.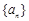 满足
满足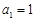 ,
,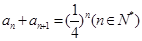 ,
,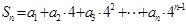 ,类比课本中推导等比数列前
,类比课本中推导等比数列前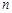 项和公式的方法,可求得
项和公式的方法,可求得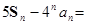 ___
___ 是等差数列
是等差数列 的前
的前 项和,且
项和,且 ,则
,则 的值为
的值为