题目内容
过点O引三条射线OA,OB,OC,已知∠AOB=θ,∠AOC=β,∠BOC=α,且平面AOB⊥平面BOC,则有
- A.cosα=cosθ•cosβ
- B.cosβ=cosθ•cosα
- C.sinα=sinθ•sinβ
- D.sinβ=sinθ•sinα
B
分析:根据平面AOB⊥平面BOC,我们可以构造直角三角形,不妨设A′B垂直平面BOC,C′B垂直平面AOB.则∠A′BO=90°,∠C′BO=90°,从而在直角三角形中,利用三角函数表示出相应的边,根据余弦定理:OA′2+OC′2-A′C′2=2OA′×OC′×cosβ,AC′2=A′B2+BC′2,将相应的边代入化简即可.
解答: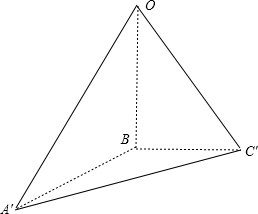 解:平面AOB⊥平面BOC,我们设A′B垂直平面BOC′,C′B垂直平面AOB′.
解:平面AOB⊥平面BOC,我们设A′B垂直平面BOC′,C′B垂直平面AOB′.
则∠A′BO=90°,∠C′BO=90°,∠A′OB=θ,∠A′OC′=β,∠BOC′=α
那么就有:OB=OA′cosθ=OC′cosα.A′B=OA′sinθ,BC′=OC′sinα.
根据余弦定理:OA′2+OC′2-A′C′2=2OA′×OC′×cosβ,AC′2=A′B2+BC′2
所以:OA′2+0C′2-[(OA′sinθ)2+(OC′sinα)2]=2OA′×OC′×cosβ…(*)
∵OB=OA′cosθ=OC′cosα
∴OA′=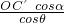 ,代入(*)中.可以得到:
,代入(*)中.可以得到:
cosβ=cosθcosα
故选B.
点评:本题以面面垂直为载体,考查余弦定理的运用,考查勾股定理,属于中档题.
分析:根据平面AOB⊥平面BOC,我们可以构造直角三角形,不妨设A′B垂直平面BOC,C′B垂直平面AOB.则∠A′BO=90°,∠C′BO=90°,从而在直角三角形中,利用三角函数表示出相应的边,根据余弦定理:OA′2+OC′2-A′C′2=2OA′×OC′×cosβ,AC′2=A′B2+BC′2,将相应的边代入化简即可.
解答:
 解:平面AOB⊥平面BOC,我们设A′B垂直平面BOC′,C′B垂直平面AOB′.
解:平面AOB⊥平面BOC,我们设A′B垂直平面BOC′,C′B垂直平面AOB′.则∠A′BO=90°,∠C′BO=90°,∠A′OB=θ,∠A′OC′=β,∠BOC′=α
那么就有:OB=OA′cosθ=OC′cosα.A′B=OA′sinθ,BC′=OC′sinα.
根据余弦定理:OA′2+OC′2-A′C′2=2OA′×OC′×cosβ,AC′2=A′B2+BC′2
所以:OA′2+0C′2-[(OA′sinθ)2+(OC′sinα)2]=2OA′×OC′×cosβ…(*)
∵OB=OA′cosθ=OC′cosα
∴OA′=
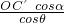 ,代入(*)中.可以得到:
,代入(*)中.可以得到:cosβ=cosθcosα
故选B.
点评:本题以面面垂直为载体,考查余弦定理的运用,考查勾股定理,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目