题目内容
若函数f(x)=-x2+2ax与g(x)=log(1-a2)(2x-1)在区间[1,2]上都是减函数,则实数a的取值范围是
- A.(-1,0)∪(0,1)
- B.(-1,0)∪(0,1]
- C.(0,1)
- D.(0,1]
A
分析:f(x)=-x2+2ax在区间[1,2]上是减函数,得[1,2]为其减区间的子集,从而得a的一个限制条件;
g(x)=log(1-a2)(2x-1)在区间[1,2]上是减函数,t=2x-1单调递增,根据复合函数单调性的判定方法,知y=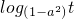 单调递减,且t=2x-1>0在[1,2]上恒成立,
单调递减,且t=2x-1>0在[1,2]上恒成立,
由此得a的另一限制条件,取其交集即可.
解答:∵f(x)=-x2+2ax的图象是开口朝下,以x=a为对称轴的抛物线,
f(x)=-x2+2ax在区间[1,2]上是减函数,∴a≤1①;
因为g(x)=log(1-a2)(2x-1)在区间[1,2]上是减函数,t=2x-1单调递增,
所以y=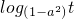 单调递减,且t=2x-1>0在[1,2]上恒成立,
单调递减,且t=2x-1>0在[1,2]上恒成立,
故有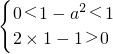 ,解得-1<a<0或0<a<1②;
,解得-1<a<0或0<a<1②;
综①②,得-1<a<0或0<a<1,即实数a的取值范围是(-1,0)∪(0,1).
故选A.
点评:本题考查复合函数的单调性、对数函数、一次、二次函数的单调性问题,具有一定综合性,复合函数单调性的判定方法是:同增异减.
分析:f(x)=-x2+2ax在区间[1,2]上是减函数,得[1,2]为其减区间的子集,从而得a的一个限制条件;
g(x)=log(1-a2)(2x-1)在区间[1,2]上是减函数,t=2x-1单调递增,根据复合函数单调性的判定方法,知y=
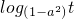 单调递减,且t=2x-1>0在[1,2]上恒成立,
单调递减,且t=2x-1>0在[1,2]上恒成立,由此得a的另一限制条件,取其交集即可.
解答:∵f(x)=-x2+2ax的图象是开口朝下,以x=a为对称轴的抛物线,
f(x)=-x2+2ax在区间[1,2]上是减函数,∴a≤1①;
因为g(x)=log(1-a2)(2x-1)在区间[1,2]上是减函数,t=2x-1单调递增,
所以y=
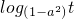 单调递减,且t=2x-1>0在[1,2]上恒成立,
单调递减,且t=2x-1>0在[1,2]上恒成立,故有
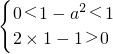 ,解得-1<a<0或0<a<1②;
,解得-1<a<0或0<a<1②;综①②,得-1<a<0或0<a<1,即实数a的取值范围是(-1,0)∪(0,1).
故选A.
点评:本题考查复合函数的单调性、对数函数、一次、二次函数的单调性问题,具有一定综合性,复合函数单调性的判定方法是:同增异减.

练习册系列答案
相关题目
若函数f(x)(x∈R)为奇函数,且存在反函数f-1(x)(与f(x)不同),F(x)=
,则下列关于函数F(x)的奇偶性的说法中正确的是( )
| 2f(x)-2f-1(x) |
| 2f(x)+2f-1(x) |
| A、F(x)是奇函数非偶函数 |
| B、F(x)是偶函数非奇函数 |
| C、F(x)既是奇函数又是偶函数 |
| D、F(x)既非奇函数又非偶函数 |