题目内容
(2013•宿迁一模)过点(-1,0)与函数f(x)=ex(e是自然对数的底数)图象相切的直线方程是
y=x+1
y=x+1
.分析:设切点为(a,ea),由f(x)=ex,f′(x)=ex,知f′(a)=ea,所以切线为:y-ea=ea(x-a),代入点(-1,0),能求出过点(-1,0)与函数f(x)=ex(e是自然对数的底数)图象相切的直线方程.
解答:解:设切点为(a,ea)
∵f(x)=ex,∴f′(x)=ex,
∴f′(a)=ea,
所以切线为:y-ea=ea(x-a),代入点(-1,0)得:
-ea=ea(-1-a),
解得a=0
因此切线为:y=x+1.
故答案为:y=x+1.
∵f(x)=ex,∴f′(x)=ex,
∴f′(a)=ea,
所以切线为:y-ea=ea(x-a),代入点(-1,0)得:
-ea=ea(-1-a),
解得a=0
因此切线为:y=x+1.
故答案为:y=x+1.
点评:本题考查利用导数求曲线上某点切线方程的求法,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
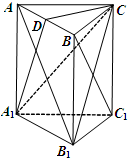 (2013•宿迁一模)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点.
(2013•宿迁一模)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点.