题目内容
下列命题正确的是( )A.
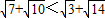
B.对任意的实数x,都有x3≥x2-x+1恒成立.
C.y=2x(2-x),(x≥2)的最大值为2
D.
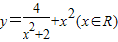 的最小值为2
的最小值为2
【答案】分析:将A中不等式两边平方,即可比较出两个数的大小,进而判断A的真假;
令x=-3,可判断不等式x3≥x2-x+1不成立,进而判断B的真假;
根据二次函数的图象和性质,分析函数的最值,可判断C的真假;
利用基本不等式,求出函数的最值,可判断D的真假.
解答:解: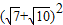 =17+2
=17+2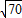 ,
,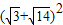 =17+2
=17+2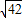 ,故
,故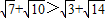 ,故A错误;
,故A错误;
当x=-3时,x3=-6<x2-x+1=-5,故对任意的实数x,都有x3≥x2-x+1恒成立,即B错误;
y=2x(2-x),(x≥2)的最大值为0,故C错误
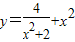 =
=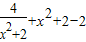 ≥2
≥2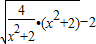 =2,故D正确
=2,故D正确
故选D
点评:本题考查的知识点是命题的真假判断,函数的最值,恒成立问题,及数的大小比较,难度不大.
令x=-3,可判断不等式x3≥x2-x+1不成立,进而判断B的真假;
根据二次函数的图象和性质,分析函数的最值,可判断C的真假;
利用基本不等式,求出函数的最值,可判断D的真假.
解答:解:
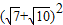 =17+2
=17+2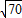 ,
,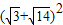 =17+2
=17+2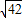 ,故
,故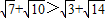 ,故A错误;
,故A错误;当x=-3时,x3=-6<x2-x+1=-5,故对任意的实数x,都有x3≥x2-x+1恒成立,即B错误;
y=2x(2-x),(x≥2)的最大值为0,故C错误
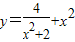 =
=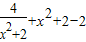 ≥2
≥2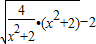 =2,故D正确
=2,故D正确故选D
点评:本题考查的知识点是命题的真假判断,函数的最值,恒成立问题,及数的大小比较,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目