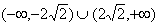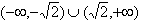题目内容
21.抛物线C的方程为(Ⅰ)求抛物线C的焦点坐标和准线方程;
(Ⅱ)设直线AB上一点M,满足![]() ,证明线段PM的中点在y轴上;
,证明线段PM的中点在y轴上;
(Ⅲ)当![]() =1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标
=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标![]() 的取值范围.
的取值范围.
21.(Ⅰ)解:由抛物线C的方程y=ax2(a<0)得,焦点坐标为(0,![]() ),准线方程为
),准线方程为
y= -![]()
(Ⅱ)证明:设直线PA的方程为y-y0=k1(x-x0).直线PB的方程为y-y0=k2(x-x0)
点P(x0,y0)和点A(x1,y1)的坐标是方程组
|
的解,将②式代入①式得ax2-k1x+k1x0-y0=0,于是x1+x0=![]() ,故
,故
x1=![]() -x0 ③
-x0 ③
又点P(x0,y0)和点B(x2,y2)的坐标是方程组

![]()
的解,将⑤式代入④式得ax2-k2x+k2x0-y0=0,于是x2+x0=![]() ,故
,故
x2=![]() -x0
-x0
由已知得,k2=-λk1,则x2=-![]() k1-x0 ⑥
k1-x0 ⑥
设点M的坐标为(xM, yM),由![]() ,则
,则
xM=![]()
将③式和⑥式代入上式得
xM=![]() =-x0,
=-x0,
即xM+x0=0,所以,线段PM的中点在y轴上.
(Ⅲ)解:因为点P(1, -1)在抛物线y=ax2上,所以a=-1,抛物线方程为y=-x2.
由③式知x1=-k1-1,代入y= x2得y1= -(k1+1)2
将λ=1代入⑥式得x2=k1-1,代入y=-x2得y2=-(k1-1)2.
因此,直线PA、PB分别与抛物线C的交点A、B的坐标为
A(-k1-1, -k12-2k1-1), B(k1-1, -k12+2k1-1)
于是
![]() =(k1+2, k12+2 k1),
=(k1+2, k12+2 k1),
![]() =(2k1,4k1)
=(2k1,4k1)
![]() ·
·![]() =2k1(k1+2)+4k1(k12+2k1)
=2k1(k1+2)+4k1(k12+2k1)
=2k1 (k1+2)(2k1+1)
因∠PAB为钝角且P、A、B三点互不相同,故必有![]() ·
·![]() <0,即
<0,即
k1 (k1+2)(2k1+1)<0,
求得k1的取值范围为
k1<-2或-![]() <k1<0
<k1<0
又点A的纵坐标y1满足y1= -(k1+1)2,故
当k1<-2时,y1<-1
当-![]() <k1<0时,-1<y1<-
<k1<0时,-1<y1<-![]()
所以,∠PAB为钝角时点A的纵坐标y1的取值范围为
(-∞,-1)∪(-1,-![]() ).
).

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
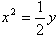 ,过点A(0,-1)和点B(t,3)的直线与抛物线C没有公共点,则实数t的取值范围是
,过点A(0,-1)和点B(t,3)的直线与抛物线C没有公共点,则实数t的取值范围是