题目内容

函数f(x)=ax-b的图象如图所示，其中a、b为常数，则下列结论正确的是(    )

A.a＞1,b＜0                      B.a＞1,b＞0

C.0＜a＜1,b＞0                   D.0＜a＜1,b＜0

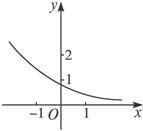
思路点拨：根据函数f(x)=ax-b的图象的单调性判断底数的范围，再与标准指数函数f(x)=ax的图象相比较在x轴方向上是向右移动了还是向左移动了来判断b的符号.

解：由图可知，y随x的增大而减小，

∴函数f(x)=ax-b是单调递减的.

∴0＜a＜1.又由于函数图象与y轴的交点在点（0，1）的下方，

即函数f(x)=ax-b的图象是由函数f(x)=ax的图象向左平移得到的.

∴-b＞0.∴b＜0.因此，选D.

练习册系列答案
相关题目
函数f(x)=
ax+2b
1+x2
是定义在（-1，1）上的奇函数，且f(1)=
1
2
．
（1）求函数f（x）的解析式；
（2）讨论函数f（x）的单调性；
（3）解不等式f(2-t)+f(
t
5
)＜0．
已知函数f(x)=
ax，(x＜0)
(a-3)x+4a，(x≥0)
满足对任意的实数x1≠x2都有
f(x1)-f(x2)
x1-x2
＜0成立，则实数a的取值范围是（　　）
已知定义在区间（-1，1）上的函数f(x)=
ax+b
1+x2
为奇函数，且f(
1
2
)=
2
5
．
（1）求实数a，b的值；
（2）用定义证明：函数f（x）在区间（-1，1）上是增函数；
（3）解关于t的不等式f（t-1）+f（t）＜0．
已知函数f(x)=
ax-1x+1
，  其中 a∈R．
（1）当a=1时，求函数满足f（x）≤1时的x的集合；
（2）求a的取值范围，使f（x）在区间（0，+∞）上是单调减函数．
已知函数f(x)=ax+
a-1x
 (a∈R)，g（x）=lnx．
（1）若对任意的实数a，函数f（x）与g（x）的图象在x=x0处的切线斜率总相等，求x0的值；
（2）若a＞0，对任意x＞0，不等式f（x）-g（x）≥1恒成立，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网