题目内容
已知直线l1:2x-y+4=0与直线l2平行,且l2与抛物线y=x2相切,则直线l1、l2间的距离等于分析:根据两直线平行时斜率相等得到直线l2的斜率,再根据l2与抛物线y=x2相切时,导函数在取切点横坐标时的值为直线斜率,列出方程求出切点坐标,然后根据切点到直线l1的距离得到直线l1、l2间的距离.
解答:解:设切点坐标是(x0,x02),因为直线l1与直线l2平行,得到斜率相等,即直线l1:2x-y+4=0的斜率为2,所以直线l2的斜率为2,
则有2x0=2,x0=1,即切点坐标是(1,1),
故直线l1、l2间的距离为切点(1,1)到直线2x-y+4=0的距离等于
=
故答案为:
则有2x0=2,x0=1,即切点坐标是(1,1),
故直线l1、l2间的距离为切点(1,1)到直线2x-y+4=0的距离等于
| |2×1-1+4| | ||
|
| 5 |
故答案为:
| 5 |
点评:考查学生理解斜率的意义,掌握两条平行线间的距离为一条直线上的任意一点到另外一条直线的垂线段的长度这个定义.

练习册系列答案
相关题目
已知直线l1:2x-my+1=0与l2:x+(m-1)y-1=0,则“m=2”是“l1⊥l2”的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充分且必要条件 | D、既不充分又不必要条件 |
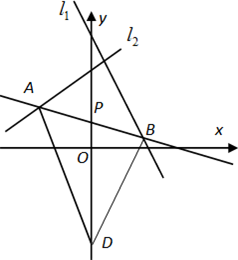 如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.
如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.