题目内容
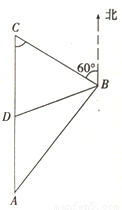
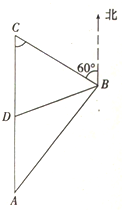某测量员做地面测量，目标A与B相距3千米，从B处测得目标C在B的北偏西60°的方向上，从A处测得C在A的正北方向，他从A向C前进2千米到达D处时，发现B、D两处也相距2千米，试求A与C的距离．分析：先利用余弦定理，求出cosA，进而求出sin∠ABC，在△ABC中，由正弦定理可求AC．
解答：解：由题意，AB=3，AD=2，BD=2，∠ACB=60°
在△ABD中，cosA=
=
∴cosA=
∴sin（A+C）=sin（A+60°）=
∴sin∠ABC=sin[π-（A+C）]=sin（A+C）=
在△ABC中，由正弦定理得，
=
∴AC=
=
即A与C的距离为
．
在△ABD中，cosA=
| AB2+AD2-BD2 |
| 2AB•BD |
| 3 |
| 4 |
∴cosA=
| ||
| 4 |
∴sin（A+C）=sin（A+60°）=
| ||||
| 8 |
∴sin∠ABC=sin[π-（A+C）]=sin（A+C）=
| ||||
| 8 |
在△ABC中，由正弦定理得，
| AC |
| sin∠ABC |
| AB |
| sinC |
∴AC=
| AB•sin∠ABC |
| sinC |
9+
| ||
| 4 |
即A与C的距离为
9+
| ||
| 4 |
点评：本题考查利用正弦定理、余弦定理在实际问题中的应用，注意选择正确的三角形以及合理的定理解答是解好题目的关键，考查计算能力，属于中档题，．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
