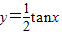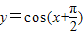Question

下列4个函数中：
①y=2008x-1；
②y=loga

2009-x

2009+x

(a＞0且a≠1)；
③y=

x2009+x2008

x+1

；
④y=x(

1

a-x-1

+

1

2

)(a＞0且a≠1)．
其中既不是奇函数，又不是偶函数的是（　　）

A．①

B．②③

C．①③

D．①④

Answer 1

分析：分别根据函数奇偶性的定义分别进行判断即可．

解答：解：①f（-x）=-2008x-1≠f（x），且f（-x）≠-f（x），∴①为非奇非偶函数．
②由

2009-x

2009+x

＞0得-2009＜x＜2009，定义域关于原点对称，且f（-x）=log a

2009+x

2009-x

=log a(

2009-x

2009+x

)-1=-f（x），∴②为奇函数．
③函数的定义域为{x|x≠-1}，定义域关于原点不对称，∴③为非奇非偶函数．
④f（x）=x（

ax

1-ax

+

1

2

）=x•

ax-1

2(1-ax)

，函数的定义域为{x|x≠0}，定义域关于原点对称，
∵f（-x）=-x•

a-x-1

2(1-a-x)

=-x?

1-ax

2(ax-1)

=x•

ax-1

2(1-ax)

=f（x），∴④为偶函数．
故既不是奇函数，又不是偶函数的是①③，
故选：C．

点评：本题主要考查函数奇偶性的判断，利用函数奇偶性的定义是解决本题的关键，要注意要先判断函数的定义域是否关于原点对称．