Question

已知函数f(x)=lnx,g(x)=ax²+bx,a≠0.

(1)若b=2,且函数h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;

(2)设函数f(x)的图象C₁与函数g(x)的图象C₂交于点P、Q,过线段PQ的中点作x轴的垂线分别交C₁、C₂于点M、N.证明C₁在点M处的切线与C₂在点N处的切线不平行.

Answer 1

(1)解:b=2时,h(x)=lnx-ax²-2x,

     则h′(x)=-ax-2=-.

    因为函数h(x)存在单调递减区间,所以h′(x)＜0有解.

    又因为x＞0,则ax²+2x-1＞0有x＞0的解.

    ①当a＞0时,y=ax²+2x-1为开口向上的抛物线,ax²+2x-1＞0总有x＞0的解;

    ②当a＜0时,y=ax²+2x-1为开口向下的抛物线,而ax²+2x-1＞0有x＞0的解,

    则Δ=4+4a＞0,且方程ax²+2x-1=0至少有一正根,此时,-1＜a＜0.

    综上所述,a的取值范围为(-1,0)∪(0,+∞).

(2)证明:设点P、Q的坐标分别是(x₁,y₁)、(x₂,y₂),0＜x₁＜x₂,

    则点M、N的横坐标为x=,

    C₁在点M处的切线斜率为k₁=,

    C₂在点N处的切线斜率为k₂=ax+b=+b.

    假设C₁在点M处的切线与C₂在点N处的切线平行,则k₁=k₂,

    即=+b.

    则=(x₂²-x₁²)+b(x₂-x₁)

    =(x₂²+bx₂)-(x₁²+bx₁)

    =y₂-y₁=lnx₂-lnx₁.

    所以ln=.

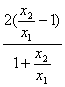    设t=,则lnt=,t＞1.                           ①

    令r(t)=lnt-,t＞1,

     则r′(t)=-=.

    因为t＞1时,r′(t)＞0,所以r(t)在［1,+∞)上单调递增.

    故r(t)＞r(1)=0.则lnt＞.

    这与①矛盾,假设不成立.

    故C₁在点M处的切线与C₂在点N处的切线不平行.