题目内容
正四面体ABCD内接于半径为R的球O,求正四面体的棱长.
思路解析:可设棱长为x、列出方程求解.关键就是确定出球心的位置.(1)一个多面体的所有顶点在一个球面上、则称这个多面体内接于一个球、这个球也叫做多面体的外接球;(2)有关外接球的问题常常利用它的轴截面来解决.
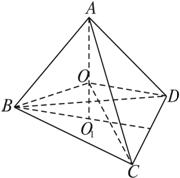
解:如图、在正四面体ABCD中、作AO1⊥底面BCD于O1、则O1为△BCD的中心.
∵OA=OB=OC=OD=R、∴球心O在底面的射影也是O1,于是A、O、O1三点共线.
设正四面体ABCD的棱长为x、
则AB=x、BO1=![]() x,AO1=
x,AO1=![]() x,
x,
∵OO1=![]() ,又OO1=AO1-AO=
,又OO1=AO1-AO=![]() x-R,
x-R,
由此解得x=![]() R,故正四面体ABCD的棱长为
R,故正四面体ABCD的棱长为![]() R.
R.

练习册系列答案
相关题目
