Question

要在宽为6米的教室当中装一盏电灯，电灯装在距离正中桌面的高是多少米时，才能使两边靠墙的课桌得到的亮度最大？（已知：电灯对课桌的照度E=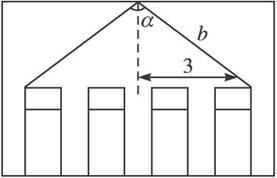cosα,I为电灯的光度，b、α如图所示）.

Answer 1

解：由题设E=及b=得E=sin²αcosα要使靠墙的课桌得到最大亮度，即E值最大.

∵是常数，且cosα的值使得（sin²αcosα）²与sin²αcosα同时达到最大值，

因（sin²αcosα）²=cos²α(1-cos²α)²

=·2cos²α·(1-cos²α)·(1-cos²α),

又由α为锐角，

且2cos²α+(1-cos²α)+(1-cos²α)=2为定值，

∴当2cos²α=1-cos²α，

即cosα=时（sin²αcosα）²最大.

亦即E最大，这时h=(米).

注：若x+y+z=k,k为定值，x＞0,y＞0,z＞0,则当且仅当

x=y=z时

xyz有最大值.