题目内容
当x∈[-2,2]时,ax<2(a>0且a≠1),则实数a的取值范围是________.
 ∪(1,
∪(1, )
)当x∈[-2,2]时,ax<2(a>0且a≠1),当a>1时,y=ax是一个增函数,则有a2<2,可得- <a<
<a< ,故有1<a<
,故有1<a< ;
;
当0<a<1时,y=ax是一个减函数,则有a-2<2,可得a> 或a<-
或a<- (舍),故有
(舍),故有 <a<1.
<a<1.
综上可得,a∈ ∪(1,
∪(1, ).
).
 <a<
<a< ,故有1<a<
,故有1<a< ;
;当0<a<1时,y=ax是一个减函数,则有a-2<2,可得a>
 或a<-
或a<- (舍),故有
(舍),故有 <a<1.
<a<1.综上可得,a∈
 ∪(1,
∪(1, ).
).
练习册系列答案
相关题目
 ,
, ,
, ,
, ,则下列等式一定成立的是( )
,则下列等式一定成立的是( )



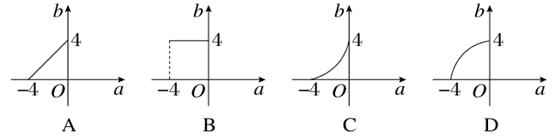
 )x是指数函数(小前提),所以函数y=(
)x是指数函数(小前提),所以函数y=(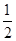 )x2+2x-1的值域是( )
)x2+2x-1的值域是( )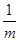 +
+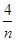 的最小值是( )
的最小值是( )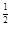 ,b=log
,b=log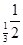 ,c=log
,c=log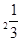 ,则( )
,则( )