题目内容
在命题“若抛物线y=ax2+bx+c的开口向下,则{x|ax2+bx+c<0}≠∅”的逆命题、否命题、逆否命题中真命题的个数
1
1
.分析:先判断原命题的真假,可得逆否命题的真假,再判断逆命题的真假,可得否命题的真假,进而可得答案.
解答:解:命题“若抛物线y=ax2+bx+c的开口向下,则{x|ax2+bx+c<0}≠∅”为真命题,
因为抛物线向下无限延伸,必存在x使y<0,,即{x|ax2+bx+c<0}≠∅,
故其逆否命题也为真命题;
其逆命题“若{x|ax2+bx+c<0}≠∅,则抛物线y=ax2+bx+c的开口向下”为假命题,
因为即使抛物线开口向上,当最低点在x轴下方时,也满足若{x|ax2+bx+c<0}≠∅,
因为逆命题和否命题的真假相同,故否命题也为假命题.
故逆命题、否命题、逆否命题中真命题的个数为:1
故答案为:1
因为抛物线向下无限延伸,必存在x使y<0,,即{x|ax2+bx+c<0}≠∅,
故其逆否命题也为真命题;
其逆命题“若{x|ax2+bx+c<0}≠∅,则抛物线y=ax2+bx+c的开口向下”为假命题,
因为即使抛物线开口向上,当最低点在x轴下方时,也满足若{x|ax2+bx+c<0}≠∅,
因为逆命题和否命题的真假相同,故否命题也为假命题.
故逆命题、否命题、逆否命题中真命题的个数为:1
故答案为:1
点评:本题为四种命题真假的判断,理解原命题和逆否命题同真假,逆命题和否命题同真假是解决问题的关键,属基础题.

练习册系列答案
相关题目
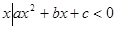 }
}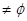 ”的逆命题、否命题、逆否命题中结论成立的是
( )
”的逆命题、否命题、逆否命题中结论成立的是
( )