题目内容
已知函数 ,若直线
,若直线 是函数
是函数 图象的一条切线.
图象的一条切线.
(1)求函数 的解析式;
的解析式;
(2)若函数 图象上的两点
图象上的两点 、
、 的横坐标依次为2和4,
的横坐标依次为2和4, 为坐标原点,求△
为坐标原点,求△ 的面积.
的面积.
(1) ;(2)
;(2)
解析试题分析:(1)由 是函数
是函数 图象的一条切线可知
图象的一条切线可知 的最大值为
的最大值为 ,故求出
,故求出 的最大值令其等于
的最大值令其等于 ,即可得到关于
,即可得到关于 的方程;(2)利用
的方程;(2)利用 的解析式求出点
的解析式求出点 的坐标, 再 求出
的坐标, 再 求出 的长,然后利用余弦定理求出
的长,然后利用余弦定理求出 的余弦值,在求出正弦值,最后代入
的余弦值,在求出正弦值,最后代入 去求△
去求△ 的面积。
的面积。
(1)

 2′
2′ 直线
直线 是函数图象的一条切线,
是函数图象的一条切线, ,解得
,解得 .
. 5′
5′
(2)由(1)知, ,
, 6′
6′ 7′
7′

 9′
9′
根据余弦定解得
 10′
10′ . 11′
. 11′ 的面积为
的面积为 . 12′
. 12′
考点:(1)三角恒等变换;(2)平面内两点间距离公式的应用;(3)利用 求三角形的面积。
求三角形的面积。

练习册系列答案
相关题目
 ;
; 的周期和单调递增区间;
的周期和单调递增区间; 在
在 上有解,求实数m的取值范围.
上有解,求实数m的取值范围. .
.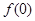 的值;
的值; ,求
,求 的值.
的值. .
. ,且
,且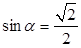 ,求
,求 的值;
的值; 的最小正周期及单调递增区间.
的最小正周期及单调递增区间. .
. ,求
,求 的取值构成的集合.
的取值构成的集合. ,求
,求 的值.
的值. -
- )-2cos2
)-2cos2 .
. ,
, .
. ,求
,求 的最大值及相应的
的最大值及相应的 的取值集合;
的取值集合; 是
是 ,求
,求 的值和
的值和 各取何值时,扇形的面积S最大?并求出扇形面积的最大值.
各取何值时,扇形的面积S最大?并求出扇形面积的最大值.