题目内容
定义在（-1，1）上的函数f(x)，①对任意x，y∈（-1，1）都有：f(x)+f(y)=f(
)；②当x∈（-1，0）时，f(x)＞0，回答下列问题:（1）判断f(x)在（-1，1）上的奇偶性，并说明理由;
（2）判断函数f(x)在（0，1）上的单调性，并说明理由;
（3）若f(
)=
，试求f(
)-f(
)-f(
)的值．
解：（1）令x=y=0f(0)=0，令y=-x，则f(x)+f(-x)=0f(-x)=-f(x)f(x)在（-1,1）上是奇函数.
（2）设0＜x1＜x2＜1，则f(x1)-f(x2)=f(x1)+f(-x2)=f()，
而x1-x2＜0,0＜x1x2＜1-1＜＜0
f(
)＞0.
即当x1＜x2时，f(x1)＞f(x2)．
∴f（x）在（0，1）上单调递减．
（3）由于f(
)-f(
)=f(
)+f(-
)=f(
)=f(
)，
f(
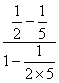)-f(
)=f(
),f(
)-f(
)=f(
)，
∴f(
)-f(
)-f(
)=2f(
)=2×
=1．
练习册系列答案
阅读快车系列答案
相关题目
＞0.
)＜f(
).
是定义在（-1，1）的奇函数，且f（
）=
．
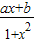是定义在（-1，1）的奇函数，且f（
）=
．