题目内容
定议在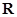 上的单调函数
上的单调函数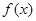 满足
满足 ,且对任意
,且对任意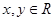 都有
都有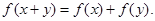
(1)求证: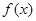 为奇函数;
为奇函数;
(2)若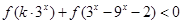 对任意
对任意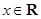 恒成立,求实数
恒成立,求实数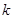 的取值范围.
的取值范围.
(1)详见解析:(2)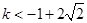 .
.
解析试题分析:(1)赋值法求解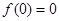 ,再寻找
,再寻找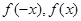 之间的关系;(2)先研究函数的单调性,再利用奇偶性化为
之间的关系;(2)先研究函数的单调性,再利用奇偶性化为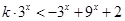 ,即
,即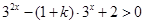 对任意的
对任意的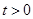 恒成立,再转化为二次函数知识求解.本题考查了恒成立问题以及化归与转化思想.
恒成立,再转化为二次函数知识求解.本题考查了恒成立问题以及化归与转化思想.
试题解析:(1)证明: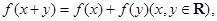 ①
①
令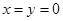 ,代入①式,得
,代入①式,得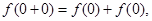 即
即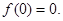
令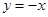 ,代入①式,得
,代入①式,得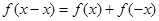 ,又
,又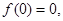
则有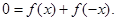 即
即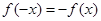 对任意
对任意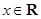 成立,
成立,
所以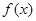 是奇函数. 4分
是奇函数. 4分
(2)解: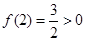 ,即
,即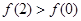 ,又
,又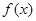 在
在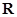 上是单调函数,
上是单调函数,
所以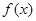 在
在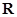 上是增函数.
上是增函数.
又由(1)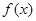 是奇函数.
是奇函数.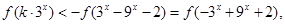
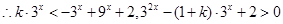 对任意
对任意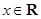 成立.
成立.
令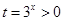 ,问题等价于
,问题等价于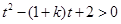 对任意
对任意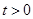 恒成立. 8分
恒成立. 8分
令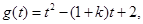 其对称轴
其对称轴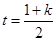 .
.
当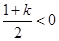 时,即
时,即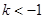 时,
时,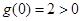 ,符合题意;
,符合题意;
当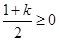 时,对任意
时,对任意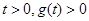 恒成立
恒成立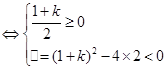
解得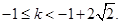 12分
12分
综上所述当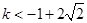 时,
时,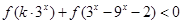 对任意
对任意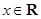 恒成立.
恒成立.
考点:1.函数奇偶性的证明;2.二次函数恒成立问题;3.化归与转化思想.

练习册系列答案
相关题目
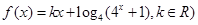 是偶函数.
是偶函数.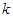 的值;
的值;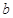 ,函数
,函数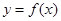 的图像与直线
的图像与直线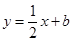 最多只有一个交点;
最多只有一个交点;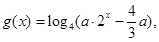 若函数
若函数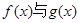 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数 的取值范围.
的取值范围.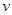 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到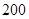 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 ;当
;当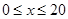 时,车流速度为
时,车流速度为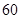 千米/小时.研究表明:当
千米/小时.研究表明:当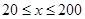 时,车流速度
时,车流速度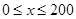 时,求函数
时,求函数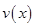 的表达式;
的表达式;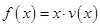 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)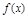 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.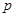 与日产量
与日产量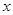 (万件)间的关系
(万件)间的关系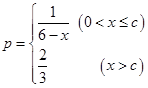 (
( 为常数,且
为常数,且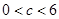 ),已知每生产一件合格产品盈利
),已知每生产一件合格产品盈利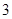 元,每出现一件次品亏损
元,每出现一件次品亏损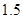 元.
元.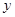 (万元)表示为日产量
(万元)表示为日产量 )
) (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式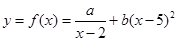 ,其中
,其中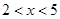 ,
, 为常数,已知销售价格为4元/千克时,每日可销售出该商品5千克;销售价格为4.5元/千克时,每日可销售出该商品2.35千克.
为常数,已知销售价格为4元/千克时,每日可销售出该商品5千克;销售价格为4.5元/千克时,每日可销售出该商品2.35千克. 的解析式;
的解析式;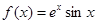 .
.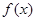 的单调区间;
的单调区间;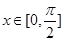 ,
,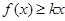 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;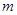 ,使得:当
,使得:当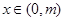 时,不等式
时,不等式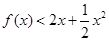 恒成立?请给出结论并说明理由.
恒成立?请给出结论并说明理由. .设某商品标价为
.设某商品标价为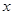 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为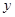 .
.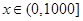 时,
时,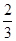 ?
?