Question

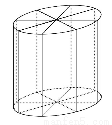
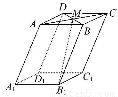
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.若M是线段AD的中点,

求证:GM∥平面ABFE.

 

Answer 1

见解析

【解析】证明：方法一:因为EF∥AB,FG∥BC,EG∥AC,∠ACB=90°,

所以∠EGF=90°,

△ABC∽△EFG.

由于AB=2EF,因此BC=2FG.

连接AF,由于FG∥BC,FG=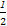BC,

在?ABCD中,M是线段AD的中点,则AM∥BC,

且AM=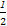BC,因此FG∥AM且FG=AM,

所以四边形AFGM为平行四边形,因此GM∥FA.

又FA?平面ABFE,GM?平面ABFE,

所以GM∥平面ABFE.

方法二:因为EF∥AB,FG∥BC,EG∥AC,∠ACB=90°,

∴∠EGF=90°,

△ABC∽△EFG.

由于AB=2EF,∴BC=2FG.

取BC的中点N,连接GN,

因此四边形BNGF为平行四边形,所以GN∥FB.

在?ABCD中,M是线段AD的中点,连接MN,

则MN∥AB.

∵MN∩GN=N,∴平面GMN∥平面ABFE.

又GM?平面GMN,∴GM∥平面ABFE.