题目内容
已知函数f（x）=4x2-mx+5在区间[-2，+∞）上是增函数，则m的范围是（ ）A．m≤-16
B．m=-16
C．m≥-16
D．m＜-16
【答案】分析：由二次函数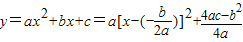
（a＞0）在区间
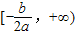上单调递增，即可求出．
解答：解：∵函数f（x）=4x2-mx+5，∴f（x）=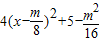
，
又已知函数f（x）=4x2-mx+5在区间[-2，+∞）上是增函数，
∴
，
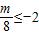解得m≤-16．
故选A．
点评：理解二次函数的单调性与二次项的系数a及顶点的横坐标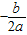
有关系是解题的关键．
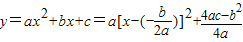（a＞0）在区间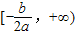上单调递增，即可求出．解答：解：∵函数f（x）=4x2-mx+5，∴f（x）=
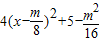，又已知函数f（x）=4x2-mx+5在区间[-2，+∞）上是增函数，
∴
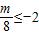，解得m≤-16．
故选A．
点评：理解二次函数的单调性与二次项的系数a及顶点的横坐标
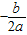有关系是解题的关键． 
练习册系列答案
相关题目