Question

S是空间四边形ABCD的对角线BD上的任意一点,E、F分别在AD、CD上,且AE∶AD=CF∶CD,BE与AS相交于R点,BF与SC相交于Q点,求证:RQ∥EF.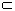

Answer 1

分析:要解决此题,需正确运用直线与平面平行的判定与性质定理.

证明:在△ADC中,AE∶AD=CF∶CD,

∴EF∥AC.

∵AC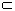平面SAC,EF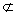平面SAC,∴EF∥平面SAC.

    又∵EF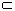平面BEF,且平面BEF∩平面SAC=RQ,

∴EF∥RQ.

点评:欲证线线平行,往往先证线面平行,再由线面平行的性质定理证得线线平行.