题目内容
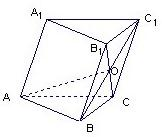已知斜三棱柱ABC-A1B1C1中，∠BAC=| π |
| 2 |
| 2π |
| 3 |
| π |
| 3 |
（1）基向量
| AB |
| AC |
| AA1 |
| AO |
（2）求异面直线AO与BC所成的角；
（3）判定平面ABC与平面B1BCC1．
分析：设
=
，
=
，
=
（1）直接表示向量
=
+
=
+
(
+
)即可；
（2）求出
，
，利用它们的数量积，求异面直线AO与BC所成的角；
（3）取BC的中点E，连接AE，推出AE⊥BC，通过
•
=0得到AE⊥BB1，证明AE⊥平面BB1C1C，即可得到平面ABC与平面B1BCC1．
| AB |
| a |
| AC |
| b |
| AA1 |
| c |
（1）直接表示向量
| AO |
| AB |
| BO |
| AB |
| 1 |
| 2 |
| BC |
| CC1 |
（2）求出
| AO |
| BC |
（3）取BC的中点E，连接AE，推出AE⊥BC，通过
| AE |
| BB1 |
解答：解：设
=
，
=
，
=
（1）
=
+
=
+
(
+
)=
(
+
+
)
（2）由题意，可求得
2=
，|
|=
，
=
-
，
•
=1，
|
|=
，cos＜
，
＞=
，
∴异面直线AO与BC所成的角为arccos
（3）取BC的中点E，连接AE，则
=
(
+
)=
(
+
)
∵AB=AC，∴AE⊥BC，且
•
=
(
+
)•
=0，
∴AE⊥BB1
∴AE⊥平面BB1C1C，AE?平面ABC，
∴平面ABC与平面B1BCC1．
| AB |
| a |
| AC |
| b |
| AA1 |
| c |
（1）
| AO |
| AB |
| BO |
| AB |
| 1 |
| 2 |
| BC |
| CC1 |
| 1 |
| 2 |
| a |
| b |
| c |
（2）由题意，可求得
| AO |
| 3 |
| 2 |
| AO |
| ||
| 2 |
| BC |
| AC |
| AB |
| AO |
| BC |
|
| BC |
| 2 |
| AO |
| BC |
| ||
| 3 |
∴异面直线AO与BC所成的角为arccos
| ||
| 3 |
（3）取BC的中点E，连接AE，则
| AE |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| a |
| b |
∵AB=AC，∴AE⊥BC，且
| AE |
| BB1 |
| 1 |
| 2 |
| a |
| b |
| c |
∴AE⊥BB1
∴AE⊥平面BB1C1C，AE?平面ABC，
∴平面ABC与平面B1BCC1．
点评：本题考查用空间向量求平面间的夹角，空间向量的夹角与距离求解公式，考查空间想象能力，逻辑思维能力，计算能力，是中档题．
练习册系列答案
相关题目
已知斜三棱柱ABC-A1B1C1的侧面BB1C1C是边长为2的菱形，∠B1BC=60°，侧面BB1C1C⊥底面ABC，∠ABC=90°，二面角A-B1B-C为30°．
已知斜三棱柱ABC-A1B1C1的侧面BB1C1C与底面ABC垂直，BB1=BC，∠B1BC=60°，AB=AC，M是B1C1的中点．
如图所示，已知斜三棱柱ABC-A1B1C1的各棱长均为2，侧棱与底面所成角为
已知斜三棱柱ABC-A1B1C1中，∠ACB=90°，AC=BC=2，点D为AC的中点，A1D⊥平面ABC，A1B⊥ACl